Thanks for the reply, @Bob. It’s cool that you did such a similar science fair project as a kid, without the benefit of all the educational resources and simulator options that exist today for Turing Tumble. My research projects were never this interesting when I was in school, to be honest. The idea to simultaneously delve into pi and mechanical computing was maybe a little over-ambitious, but it’s certainly led to a lot of discovery. Malcolm has been doing science fairs annually since first grade (even last year, remotely with COVID), so he has a lot of experience with the process and the expectations. In his case, it’s a bit different, since he’s in an accelerated academic program where they dedicate about four months each year to the science fair, with structured deliverables, etc.
Malcolm went into this project assuming that he would be able to automate the entire process, but he’s since realized that this was an unrealistic goal. He is now resigned to an approach that allows for a degree of human intervention, and this is now reflected in his problem statement. As with many historical calculation methods, the operator is an essential element of the solution. The ‘program’ is executed by following a predetermined (scripted) series of steps and copying register values from one ‘subroutine’ to another. Documenting the steps may prove challenging, but we’re looking at the assembly language for the Intel 8085 microprocessor as a template for this, due to its relative simplicity and low-level representation of basic computing operations. There’s even a simulator available…
After considering numerous potential approaches (mainly infinite sequence formulas, such as Nilakantha’s Series), we ultimately selected the Rabinowitz-Wagon spigot algorithm. As noted in the original post, there are other bounded and unbounded spigot alternatives that have been touted as ‘faster’ from a Big O perspective, but where the storage and/or calculation requirements are seemingly excessive for TT implementation.
Here’s a link to the original published article, describing the Rabinowitz-Wagon spigot algorithm in base-10:

The methods described in the paper are based on the Wallis product for π, which can be transformed into:
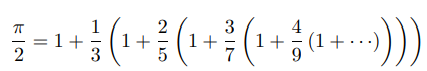
The algorithm essentially articulates the process for converting the mixed-radix terms above into base-10. This can be depicted via a table, with the fractional coefficients shown in the column headers:
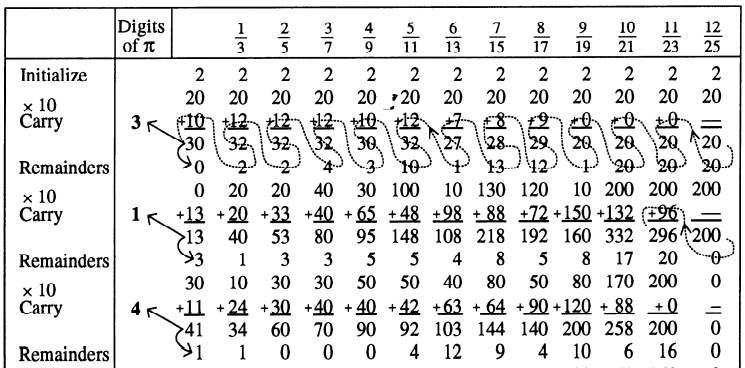
Assuming that we’re interested in calculating the first n digits of π (including the integer portion: 3), we need roughly n × π columns in the table. For each of the n rows (i.e., for each major spigot iteration, which yields another decimal digit), this sets up a series of steps to be carried out from right to left, with i = (10n div 3) + 1 to 1, corresponding to the numerator a = i - 1 and denominator b = 2i - 1 (1/3, 2/5, 3/7, 4/9, etc.).
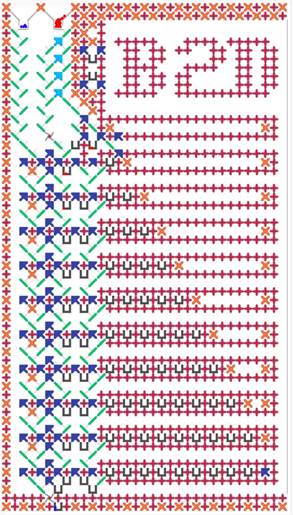
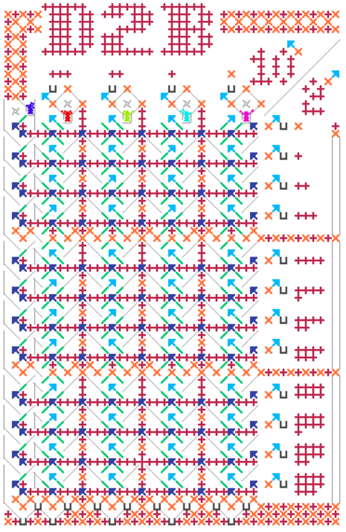
Back to the implementation in TT… Here are the specialized boards that we are developing in @jcross’s Turing Tumble Simulator*, to handle the required calculations and data storage requirements for the spigot algorithm:
-
PI Digits (storage of 4-bit BCD digits, e.g., for n = 21)
-
RW Storage (storage of the following, for each step i):
-
M1: numerator a = i - 1 (7-bit)
-
M2: denominator b = 2i - 1 (8-bit)
-
M3: initialized base (2) | r[n - 1] (6-bit)
-
M4: carry from [i] to [i - 1] (10 bit)
-
M5: main array A (12-bit)
-
M6: quotient q = A[i] div b (6-bit)
-
M7: remainder r = A[i] mod b (6-bit)
-
RW Process (persists i, M4, and M7 for all steps i)
- with pointer to i represented by a ring counter
-
Binary Arithmetic (capable of the following operations):
-
integer addition (a + b, 12-bit with overflow)
-
integer subtraction (a - b, 12-bit with underflow)
-
integer multiplication (a × b, 12-bit with overflow)
-
integer division (a div b | a mod b, 12-bit with underflow)
-
integer comparison (a == b, leverages subtraction a - b)
-
2’s complement (s2c a, used for subtraction and division)
-
Stack (accommodates up to 8 12-bit registers, with stack pointer)
-
BCD to Decimal Converter (4-bit BCD, 0-9 with overflow)
-
Decimal to Binary Converter (12-bit output with overflow)
We will provide simulator links for each of these in a future reply to this post, along with screenshots, design commentary, and basic instructions for use. It’s good to know that there’s some interest in this topic here in the Community, but it’s a valuable exercise regardless. This is basically the same information that he will need to provide as part of his science fair report. Being able to clearly articulate his methodology in writing is key, in order to communicate the mathematical underpinnings, as well as the TT-specific aspects of the solution.
–Brian
* Kudos  to @jcross [Jesse Crossen] for his ridiculously useful and engaging simulation tool. We especially appreciate the schematic mode, which is indispensable when dealing with TT boards that are upwards of 10x the standard game-board dimensions, with ~100 balls potentially in play. We also rely heavily on the PNG export/import functionality. We found a few bugs in the software, but these are easy to work around, and we certainly couldn’t have done this project without the large-board support and non-standard ball release capabilities. I can’t believe I was originally planning to take this on myself via rigid-body simulation in Blender…
to @jcross [Jesse Crossen] for his ridiculously useful and engaging simulation tool. We especially appreciate the schematic mode, which is indispensable when dealing with TT boards that are upwards of 10x the standard game-board dimensions, with ~100 balls potentially in play. We also rely heavily on the PNG export/import functionality. We found a few bugs in the software, but these are easy to work around, and we certainly couldn’t have done this project without the large-board support and non-standard ball release capabilities. I can’t believe I was originally planning to take this on myself via rigid-body simulation in Blender… 


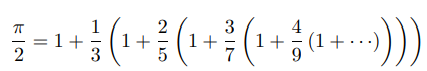

 to
to