In the beginning, each block is described.
The parts are described as follows.
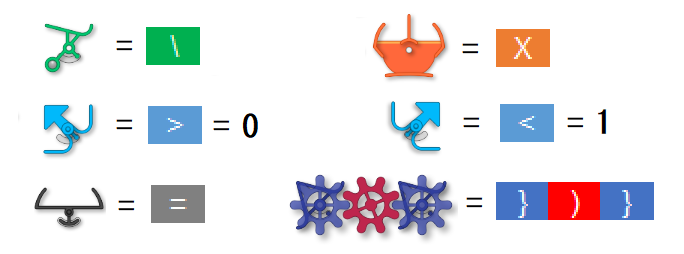
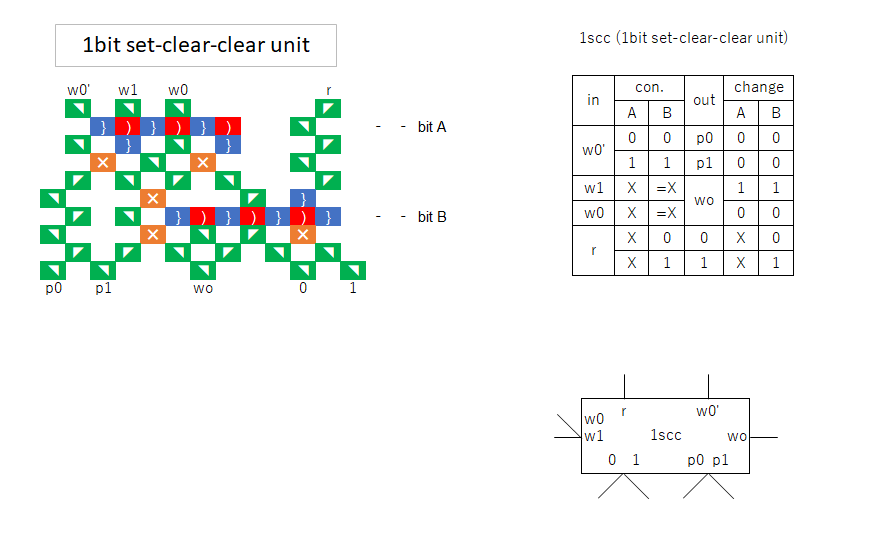
“rw” is a block that has read-write functionality.
Arrange the gear bit chains, which are independent of each other, according to the number of bits.
In the example of how to assemble the parts, I wrote with 4 bits, but in reality, 8 bits are used.
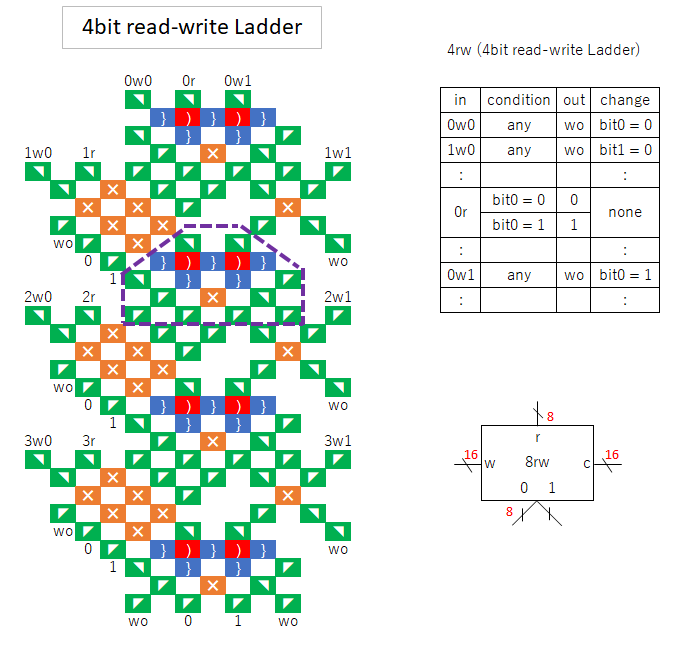
“rwP” is similar to “rw”, but branches depending on the bit when reading.
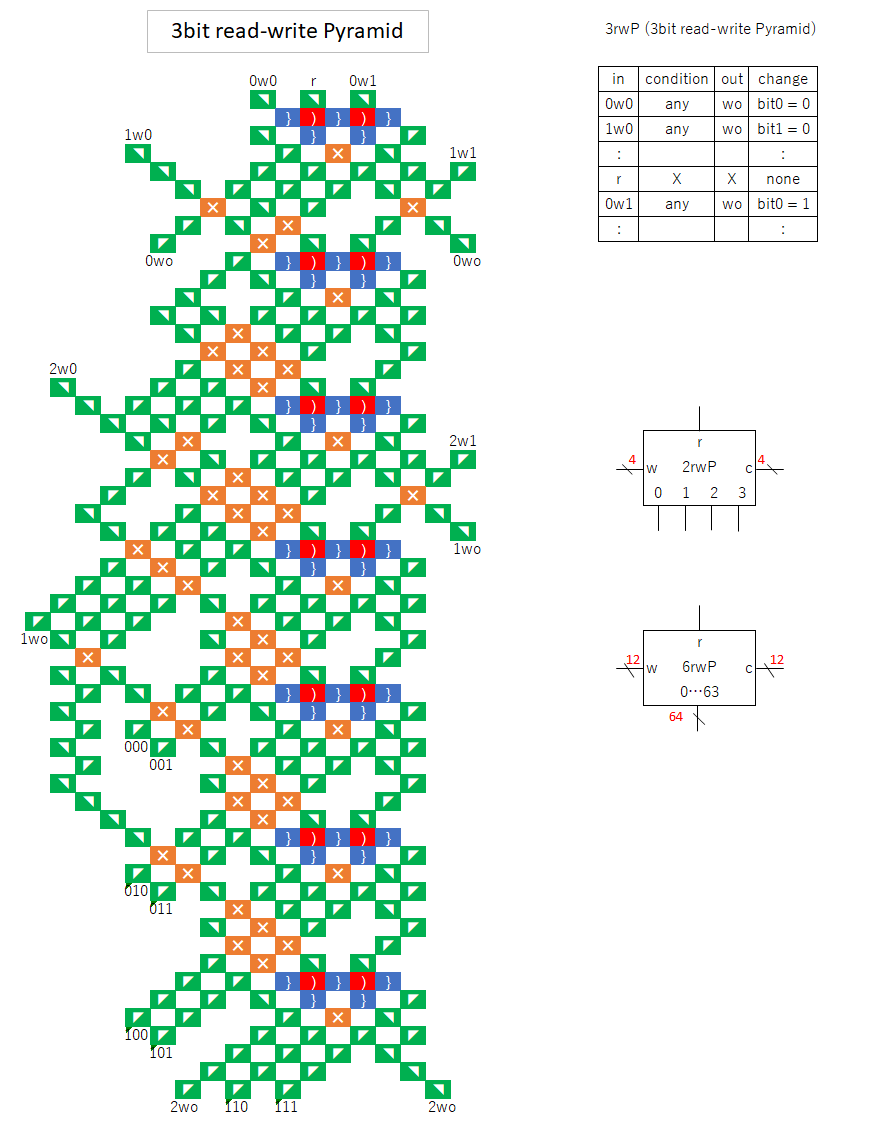
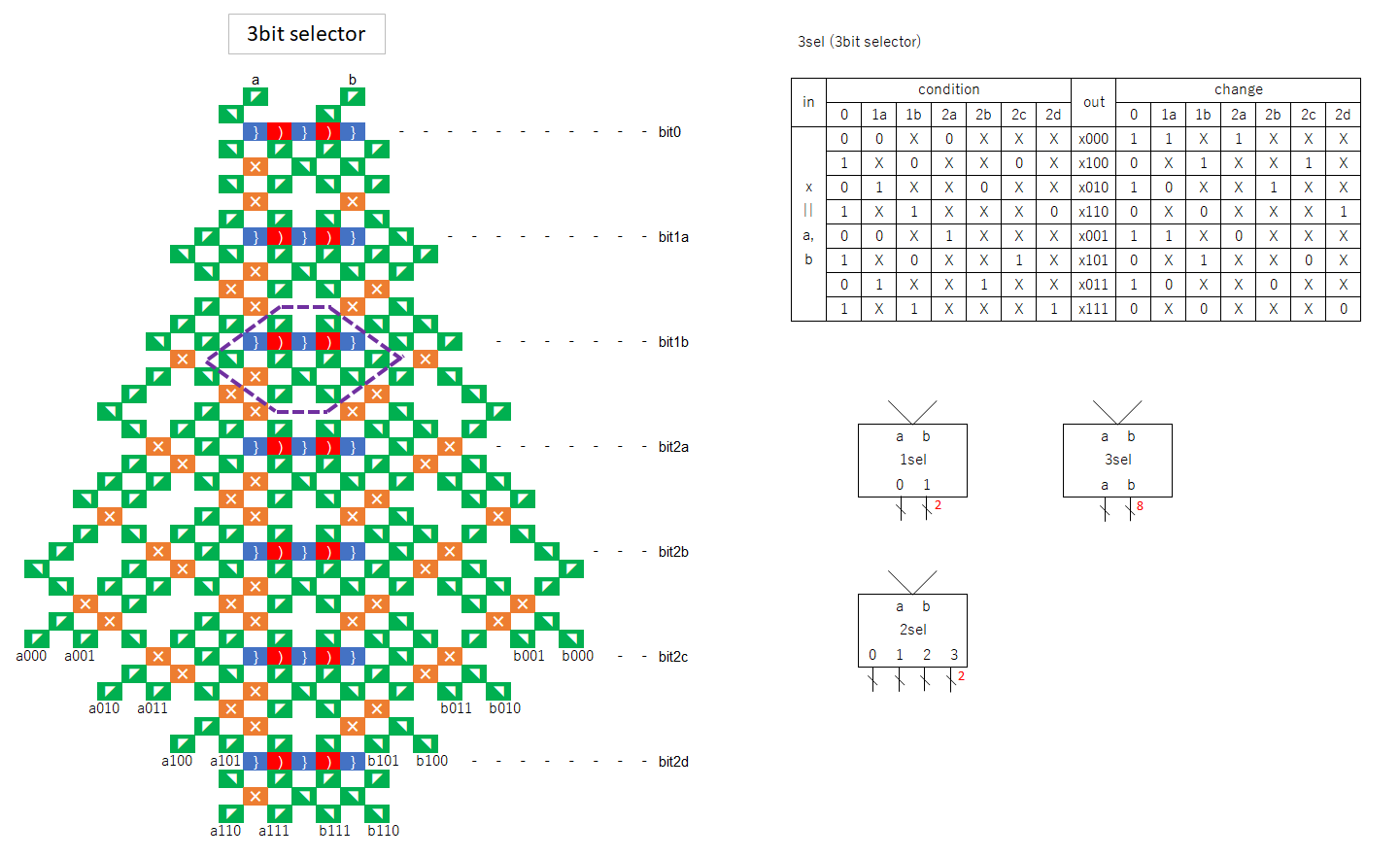
To achieve this function, the number of gear bit chains is 2^bit-1.
For example, if it is 2 bits, there are gear bit chains a and b corresponding to bit 2.
When writing, the same bit is written to a and b.
When reading, if bit1 is 0, it goes to a, if it is 1, it goes to b, and so on, following the tournament table in reverse order.
When building a CPU, either a 2-bit one or a 6-bit one is used.
“add” is a block with an additive function.
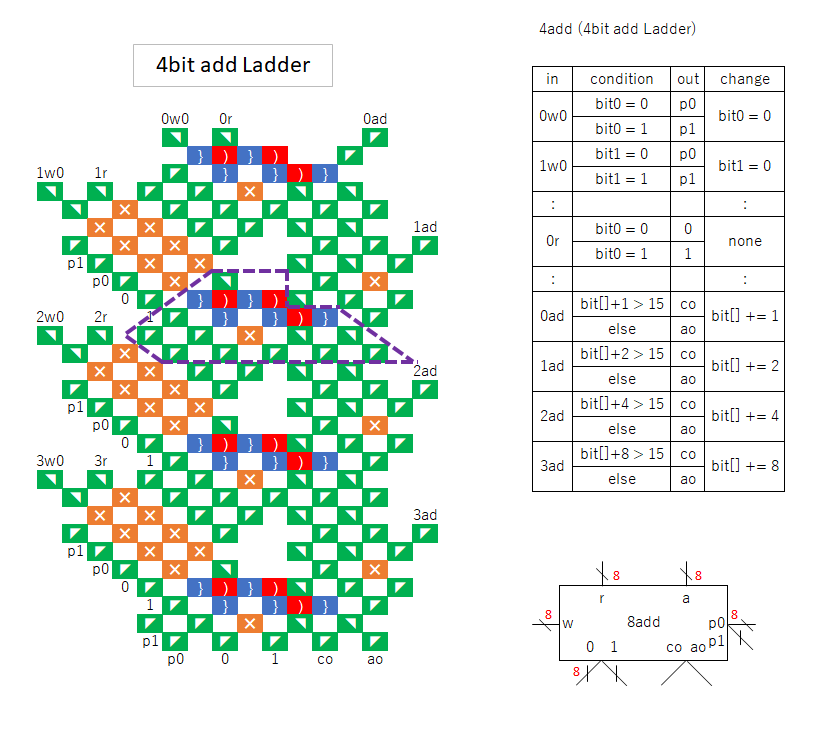
It is similar to “rw”, but instead of writing 1, it adds according to the bit.
Because of the carry, the input of +1 comes from one of the two outputs with or without carry, regardless of the bit.
In CPUs, 8-bit ones are used for addition instructions.
“addP” is a bitwise branch of “add”.
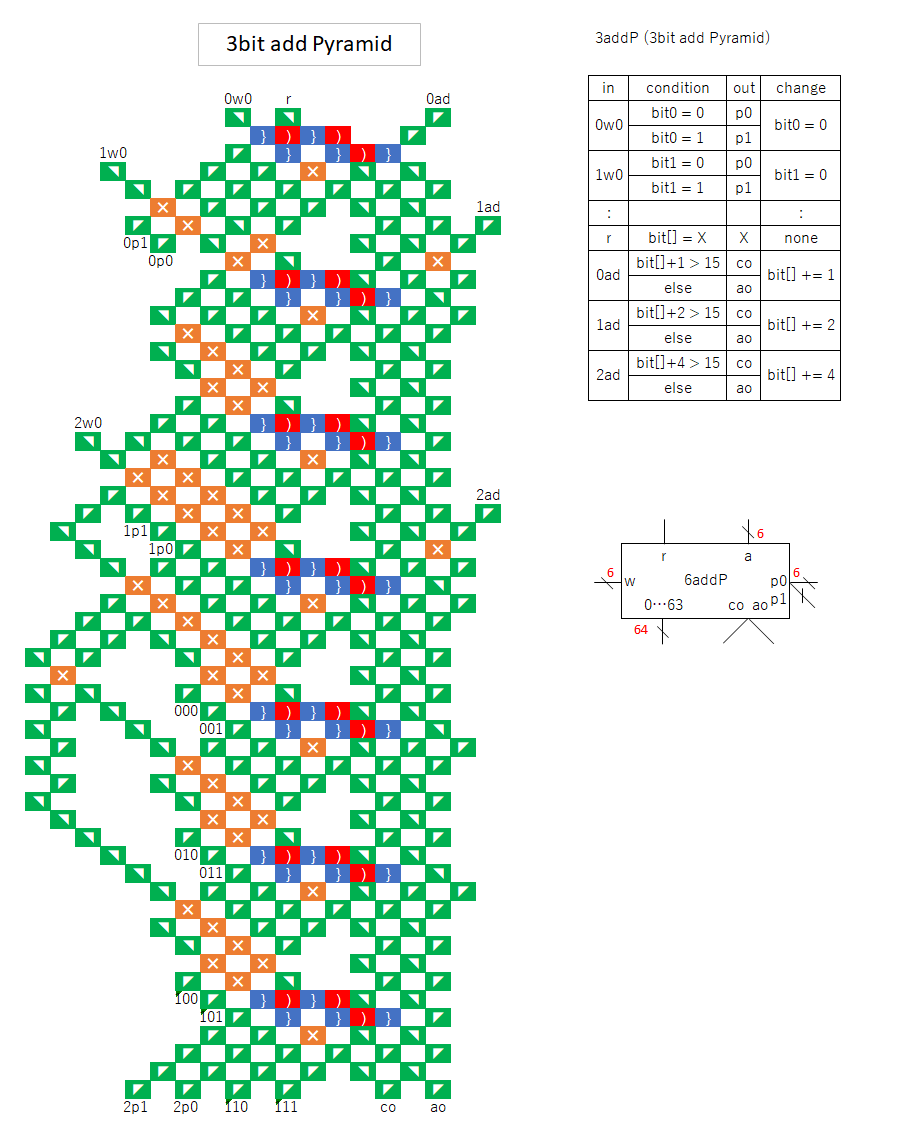
Use a 6-bit program counter, and select the one with the specified address from 2^6 memories.




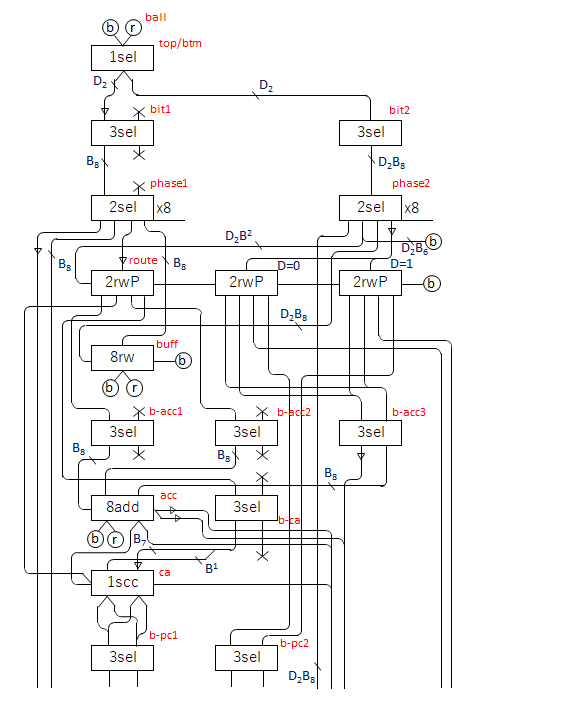
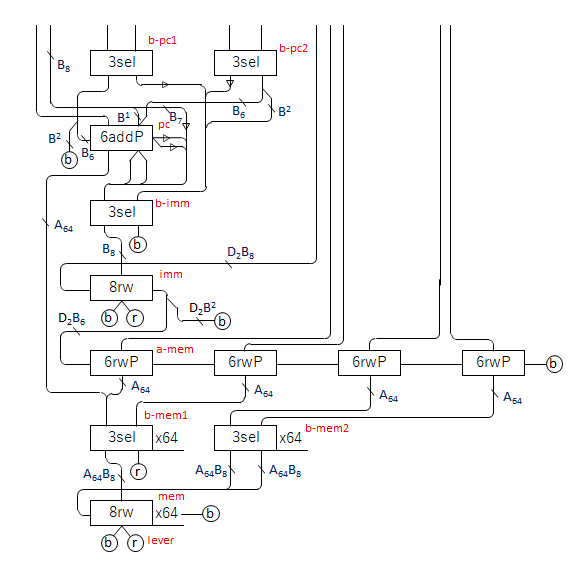
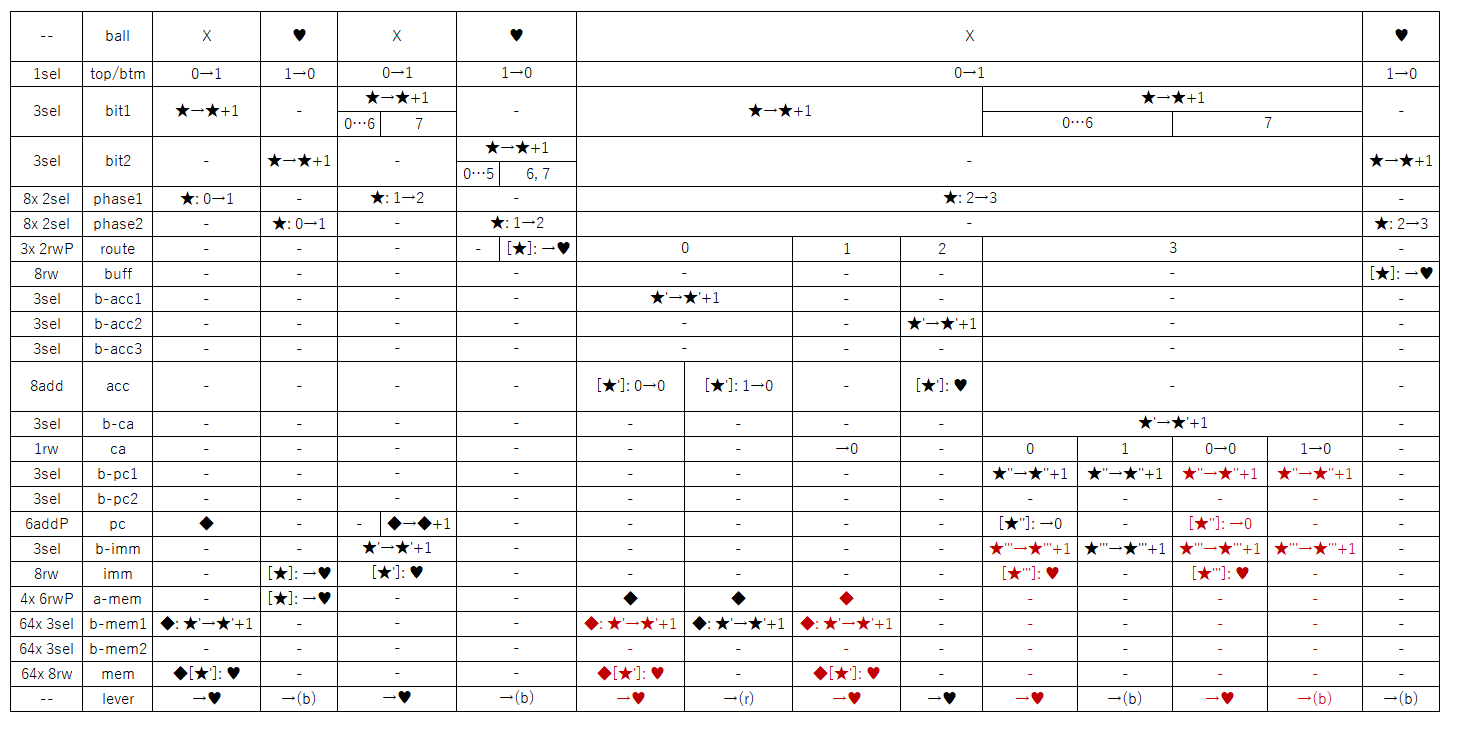
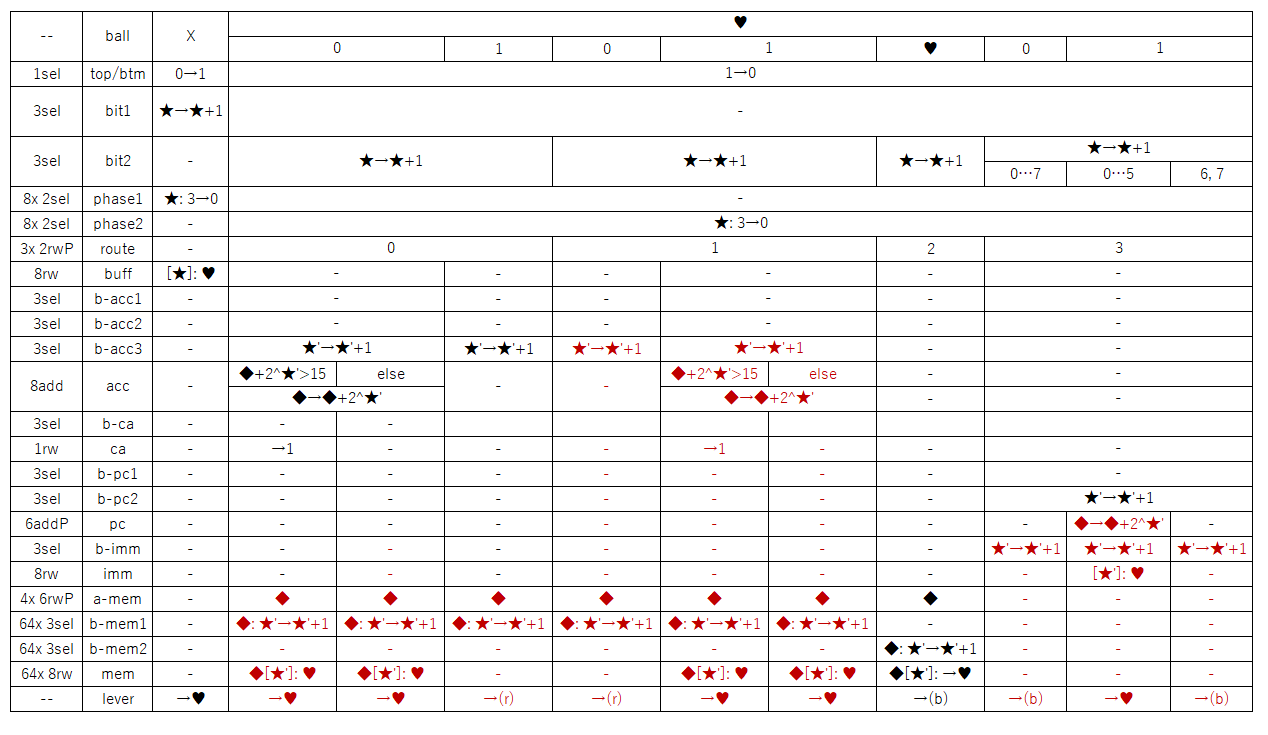
 of that memory is the output of this sequence of events, and will be the color of the next ball.
of that memory is the output of this sequence of events, and will be the color of the next ball.