Create a "Count-Once" Widget (a tool to create any sequence)

[lennypitt]

A useful “Count-Once” widget.

Often somebody will present a challenge to construct a pattern containing some number (say B1) of blue balls followed by some other number (say R1) of red balls followed by some other number (say B2) of blue balls, followed by R2 red balls, and so on, so that the output looks like:

Rn Bn Rn-1 Bn-1 … R3 B3 R2 B2 R1 B1.

For example, the challenge of producing a Fibonacci sequence
B1 = 1
R1 = 1
B2 = 2
R2 = 3
B3 = 5
R3 = 8
and so on.

It dawned on me that what is needed is a widget that can count out a certain number n of balls of a given color, but then the widget is just ignored and future balls just pass through without any effect. If we can build such widgets, then we can stack them to get any sequence of reds and blues we’d like.

EXAMPLE:
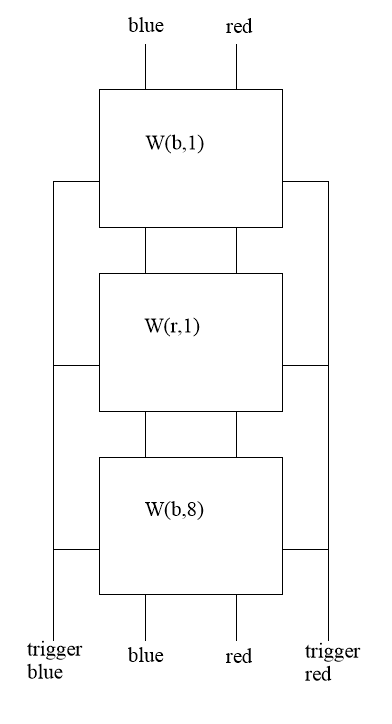
Let’s write “W(b,n)” to indicate one of these widgets that counts out n blue balls, and “W(r,n)” one that counts out n red balls. (By “counts out” I mean that it triggers n balls of the given color, then after that, lets balls pass through it without any effect.)

By building a stack of these widgets as follows, we can solve the Fibonacci challenge, and, any challenge, for that matter (assuming we are not constrained to using the original board and box parts).
Below, the widgets are arranged vertically in a tower, with W(b,1) at the top,
and all balls pass through all widgets.

W(b,1)
W(r,1)
W(b,2)
W(r,3)
W(b,5)
W(r,8)
W(b,13)
W(r,21)
and so on.

With such a stack one blue ball is counted out, then red is triggered and all future balls pass through the W(b,1) widget.
Then the W(r,1) widget counts out 1 red ball, triggers a blue ball, and all future balls just pass through it.
Then the blue ball passes through the W(b,1) and W(r,1) widgets, and enters the W(b,2) widget, which counts out another blue ball, then triggers a red, and all future balls just pass through the W(b,2) widget. Etc.

I hope I’ve explained this clearly enough.

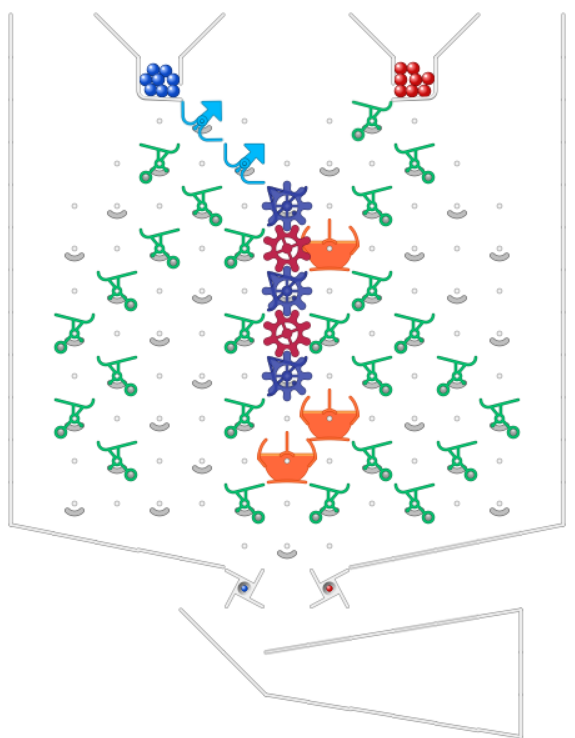
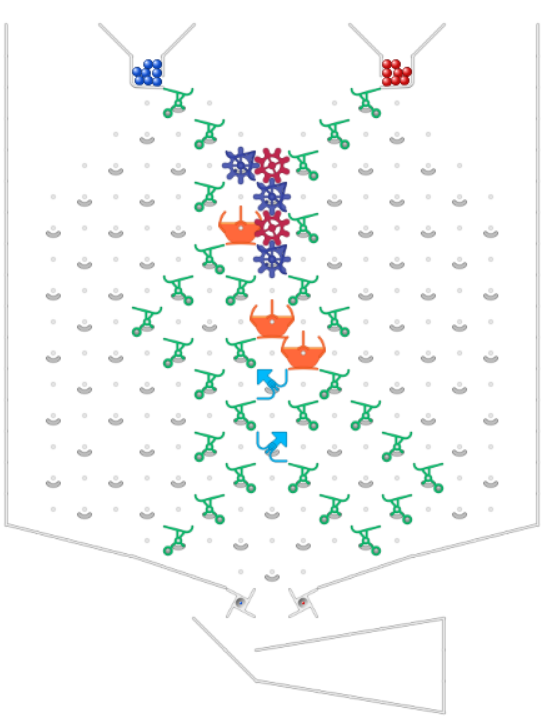
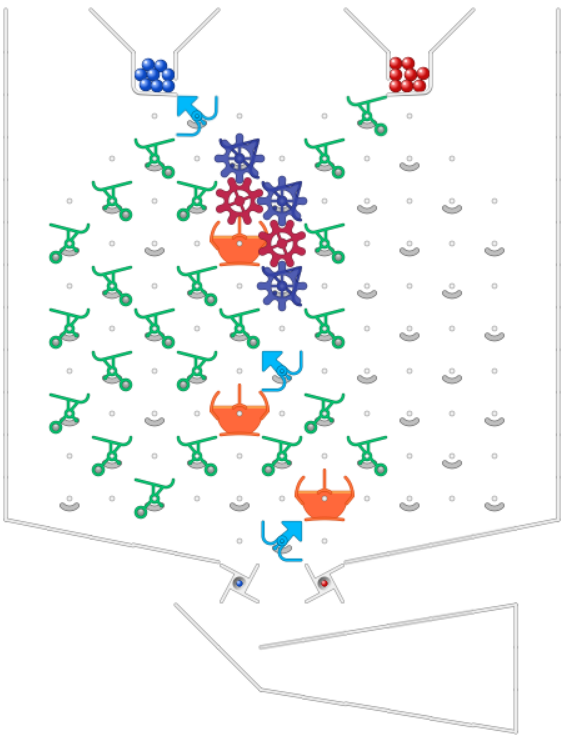
So, the challenge is to show how to build one of these widgets:

As a concrete example, build W(b,5). It should have the following behavior.
You push the blue lever.
More blue balls are triggered, then after that reds are triggered.
The output sequence is 5 blues, then repeating reds in perpetuity.
(So, the ball lineup at the bottom looks like … rrrrrrrrrrrrrbbbbb)

I did this with the simulator, but the window accidentally closed, and I’m too lazy to do it again (for now). I figure I’ll let somebody else show their solution.

[Bob]

My solutions for a W(b,5) have too many gears and gear-bits to work on a real board. I had to rotate the parts by hand to complete a test. The end state is shown. One of the gear-bits must be rotated ccw to initialize the parts.

[lennypitt]

That looks great - I think significantly smaller than my solution, but essentially using the same idea of a counter (the two regular blue bits), which after overflow (on the fifth blue ball), sets the gear bits up top to the “1” position, thereby funneling all future balls to the right.

W(b,6) would be essentially the same structure, but you’d use three blue bits (allowing counting up to 8), and initialize the counter to 2 (so the 6th blue ball would cause the overflow).

By building a similar widget underneath the bottom right ramp, you could have W(r,n) for whatever number n you wanted. Then another widget below and to the left you could have W(b,m), and so on, alternating sides, and achieving any output sequence you’d like (if the board were long enough). If you wanted to terminate the output, you could just have the final overflow feed into an interceptor.

Does this make sense?

[Bob]

My solution and your description miss an important point. The first ball into my blue-counting widget was blue. The first ball into the subsequent red-counting widget will be blue instead of red.

Each widget needs to have three outputs: trigger blue, pass (or intercept), and trigger red. My blue widget needs to add a pair of linked gear-bits to the right. I don’t have enough parts so I’ll use the simulator to add the new control and add another bit in the counter.

Tumble Together

The top gear-bit affects the bit counter so the range of this blue widget is n = 1 to 9. To initialize for n = 2, set counter to 7 (all bits cw), set top gear-bit ccw, and set right gear-bit ccw. Start with a blue ball. There is no widget below this one so an interceptor was added to catch the first red ball passing through.

Initialization for n = 1 is a special case. The counter is not used so may be any value. Set top gear-bit cw and set right gear-bit ccw. The first blue ball will trigger a red ball.

[lennypitt]

I agree - I had overlooked that. A minor point - note that the overflow ball which sets the top-gear state of the currently active widget to 1 (= “pass through”) can be routed to trigger the opposite color, so that in your example, the eighth blue ball triggers red, instead of a ninth blue.

[Bob]

I didn’t like using a long gear-bit chain to feed overflow status to the top of the widget. It was too long to work with a two-bit counter and it was worse as the count increased. I thought about using a ball-release as feedback and came up with a new widget design that works with a real game board. The key concept for a blue widget is to use the first red ball to switch to pass-mode.

As shown below, new widgets have separate inputs and outputs for blue and red balls. Two additional outputs are used to trigger a blue or red ball-release. Interceptors would be added to capture red or blue balls from the last widget to end the sequence.

The following simulator setup shows a single stage W(b,1). The 3-bit counter can be set for 1 through 8. It runs well on my physical game.

Tumble Together

I assume a red widget would mirror the layout of a blue widget. I don’t think I’ll spend more time on this project though.

[lennypitt]

That’s a nice variation. Another thing I’ve been thinking of is if the output pattern desired is just a numerical sequence, instead of a pattern of red and blue balls, the blue marbles can enumerate the sequence while the red marbles can be separators. So, we’d only need blue widgets, and the overflow could trigger a single red ball to set the “pass-through” bit. I haven’t thought the details through, but like you, am going to move on.

I’m happy knowing that we have a general technique to generate any desired pattern, that doesn’t have to rely on the even more general techniques of constructing a computer, or a Turing machine, as in other posts.

[Bob]

The design of the gear-bit chain that controls the widget might not be obvious to me in a few weeks so I attached an explanation.

[smith123]

Hello. First, I’m new to the community. Second, I have found the W(r, 1) that @Bob asked for. Here is the simulator link.Tumble Together

[George167]

Finally, I completed a solver to solve this problem using gears. Here’s what happened for W(b,4) on 5 parts. Same idea, same implementation.

W(b,3,r,1)

@lennypitt

So, we’d only need blue widgets, and the overflow could trigger a single red ball to set the “pass-through” bit. I haven’t thought the details through, but like you, am going to move on.

The computer solver does it quickly, but interpretation requires some effort. Here is a solution without optimization for W(b,3,r,1). “BBBR BBBBBB…RRRRRR…”

W(b,5,r1)
One of 11 solutions.