My first puzzle (;
starting setup Tumble Together.
make pattern blue blue red red blue blue red red…
(bit can point any way).
start with blue.
infinite ramps, 3 bits, 4 crossovers.
1 Like
Hola, he encontrado este rompecabezas y voy a colocar una solución para la serie 2 azules, 2 rojos que permite generalizarla a otro tipo de series como 3,3 ; 4,4 ; 5,5 etc.
Ejemplos para otras series:
Para serie 4🔵4🔴
Poner un contador descendente iniciado en 3 
en 
y un contador simétrico en 
conectar el bit2 que esta a 0 mediante 
—————————
Para serie 6🔵6🔴
Poner un contador descendente iniciado en 5 en y un contador simétrico en conectar el bit1 que esta a 0 mediante
——————
Para serie 7🔵7🔴
Poner un contador descendente iniciado en 6 en y un contador simétrico en conectar el bit0 que esta a 0 mediante
The second crossover isn’t necessary, as no balls will ever be routed through it.
Well, yes, that is tidier than my solution (in fact, that’s the solution for puzzle 10 in the book), but I guess I have to use the starting setup, that c5TUMBLE provided in the question.
Maybe I can solve it a little bit different, so that the crossover is used somehow.
I made a new version, that uses the starting setup from the question and the crossover.
I greyed out the pieces of the starting setup to make it clear, which pieces have to stay as they are.
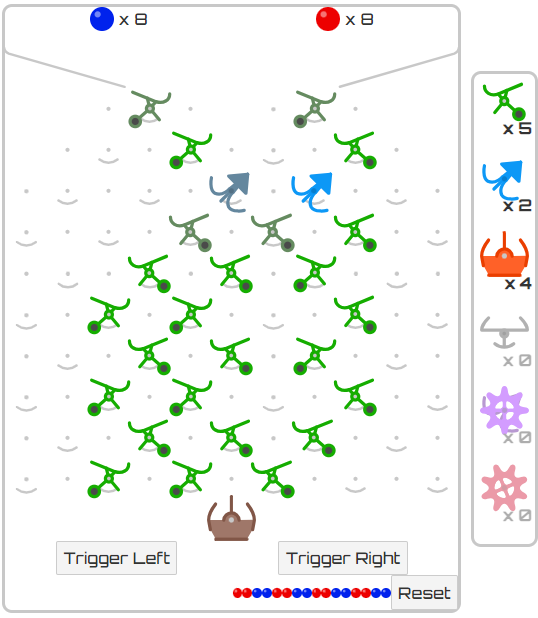
Ahh, yes. My mistake…I hadn’t read the original problem, and thought the puzzle was to simply produce the sequence
bbrrbbrrbb… Without additional constraints.
1 Like
its just the max you can use less if you want
Thanks to all the people who tried my puzzle 
1 Like