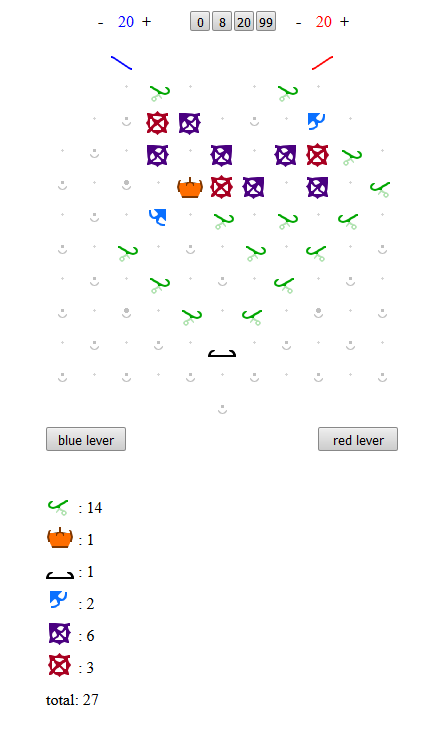
Here’s another “binary input” challenge.
The challenge is to determine if a binary input is divisible by four. The binary input is entered by feeding one ball at the time, where each ball represents a bit, its value determined by its color. You can decide which color represent the 0-bit, and which represent the 1-bit. It does not really matter. The least significant bit is entered first. There is no restriction on the size of the input. At any time, the board should indicate if the number entered so far is divisible by four.
No prize for originality as the problem statement is very similar to the divisible-by-three problem posed by @lennypitt. However, establishing that there actually exists a solution on a normal-sized Turing Tumble board is not easy.
At first glance, the problem may not look that hard, given that four is a power of two. However, as you start solving it, I think you’ll find that it is not so straightforward. It requires a different approach than the divisible-by-three problem. The real difficulty is to devise a solution that fits on a normal-sized board. It is possible though. Can you manage?
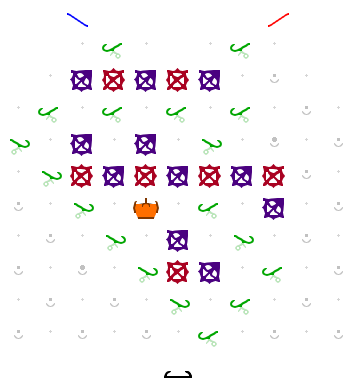
 (Not sure how to treat null, or whether “00” is a fair input, since we don’t write numbers with leading 0s. We don’t have this problem if we’re entering numbers most significant bit first.)
(Not sure how to treat null, or whether “00” is a fair input, since we don’t write numbers with leading 0s. We don’t have this problem if we’re entering numbers most significant bit first.)