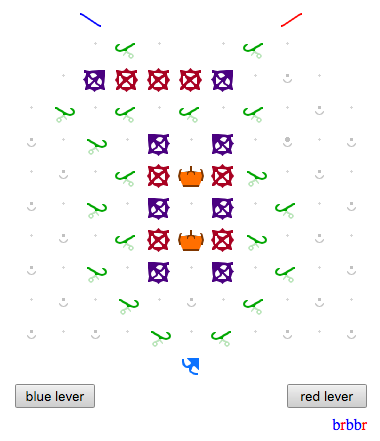
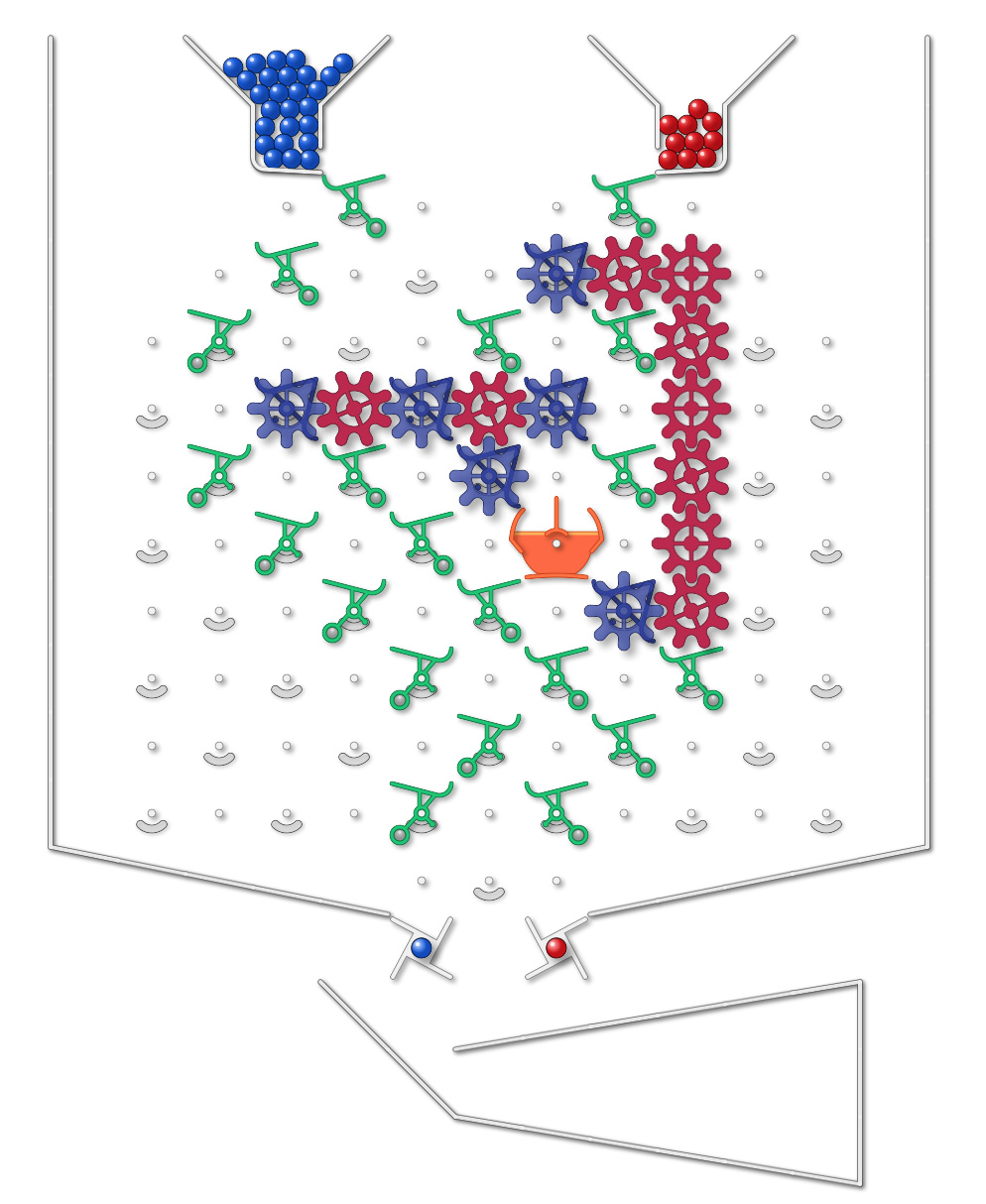
Most of the puzzles use data represented by bits on the board, which of course makes a lot of sense, and the balls are mostly used to drive the computation. But there is a whole class of other puzzles we can consider if we view the blue/red ball sequence as data. Assume that all balls are intercepted, and that the user presses a lever for each ball to be released. Let blue = 1, and red = 0. Then the user can input a number like 6, for example, by pressing blue, blue, red, since 110 = 6 in binary.
The puzzle types I’m imagining are those where the objective is to determine whether the sequences entered by the user meets some specified condition, and the answer is reflected somehow on the final board configuration.
An easy example is just “is the (binary) number the user input an even number?”. This just tests whether the last marble was red or not, and the result can be shown with a single bit.
Here is a harder one: “Is the (binary) number the user input divisible by 3?” I’ve solved that with lots of parts and a large board using the emulator, and a link is in another thread. I’m curious if there is a simple solution that can actually be done on the physical gameboard, so ask it here.
I can imagine lots of puzzles. Here are five more beyond the divisible-by-three:
- Equality: Did the user enter an equal number of reds and blues? (This can be solved, assuming a bound on reds and blues, using a solution of another puzzle appearing elsewhere on the forum.)
- Two-for-one: Did the user enter twice as many reds as blues? (An extension of the same solution. Again, assume a bound on the number.)
- Alternation: Did the user enter an alternating sequence brbrbrbr…? Or did they deviate from that pattern?
- Prime: Was the binary number entered a prime number less than 15 (we need the bound, otherwise it is impossible).
- Encoding: This one isn’t a yes/no condition, but rather to have register A, when done, reflect the binary value input by the user.
- Create-your-own: your puzzle here.