you can only use one ball, to add two 4-bit numbers.
hint: the interceptor acts as a 5th bit
1 Like
Nice challenge. I have made a few adders and didn’t think this was possible until you posed the question. How to propagate the carry bit while adding each pair of bits was not obvious at first. I love the elegance of my final solution.
Click to Reveal Solution
The purple cogs are one input and the blue bits the other. The result goes in the blue register. The left interceptor is the 5th bit or overflow bit.
I have two videos to demonstrate 6+3=9 and 5+11=16:
https://photos.app.goo.gl/1RyMtrRXERxmJQkcA
2 Likes
Awesome challenge!
Here is a slight variation on the solution given by @Rob
I found a way to sort of make it subtract as well (using 2’s complement).
Click to Reveal Solution
Just like in @Rob’s version, the value in the purple cogs register is being added to the value in the blue register. However, by dropping a blue ball instead of a red one, an additional 1 will be added to result using the carry to the initial set of purple cogs.
There is a well know trick for subtracting binary numbers. If you flip all the bits and add 1, you effectively get the negative of the number. Thus, you can use this circuit to subtract by first manually flipping all the purple cogs, and then dropping a blue ball.
For example, if you want to subtract 3, set the purple cogs to 0011 (from top to bottom) instead of 1100 (i.e. flip the bits), then drop a blue ball.
When using this circuit to add, the left interceptor represents overflow. But when using the circuit to subtract instead, the right interceptor represents underflow.
I’d love to see a version of this where the flipping of the bits is taken care of automatically instead of manually!
2 Likes
Hmmm… that’s a cool challenge!
cool! I didn’t know about 2’s complement. very interesting.
If we use ramps instead of gear bits, we can build a fast multiplier. The result in the blue register will be the product of the green register and the number of red balls.
Example: 3 x 10 = 30
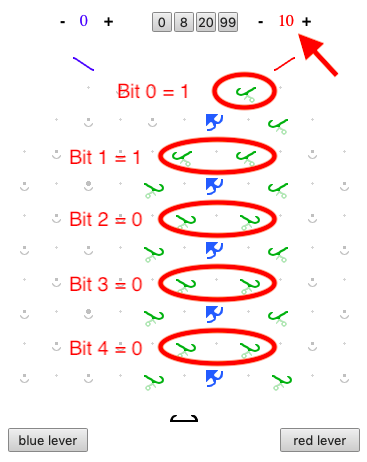
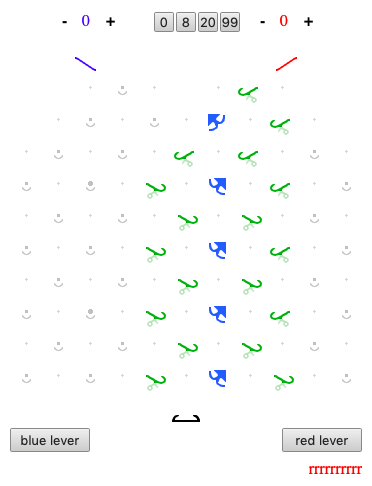
https://lodev.org/jstumble/?board=elee0leellfr0lfrrfr0lfrrfr0lfrrfr0rei_0_10
Of course, it’s faster to use the balls to represent the smaller of the two numbers (e.g. set the green register to 10 and used 3 balls).
2 Likes