Here’s my solution (it’s the one from the book):
And here’s the link:
http://www.lodev.org/jstumble/?board=rrelelebereelg1elerbrreelellererreelerlereexeelellel
Description: This is a tricky little circuit. Normally, 2 bits run a course of 4 different positions before repeating. But with this configuration, in one of the positions, one ball advances through two of the positions at once, causing there to be only a 3 position cycle.
Here’s a video of an alternative solution to Turing Tumble Challenge #39 which is less complex. It uses only 19 parts (if I counted correctly). 17 of those are simple ramps and the other 2 are bits. No gear bits or other complex parts are required.
Damn, that’s neat. You should totally post that in a separate thread with a jstumble link. Also, you can get that down to 13(!) parts by merging the blue and red path at the top and moving the bits all the way to the bottom:
It’s a neat way of getting the required pattern, but it doesn’t actually solve challenge #39 which specifies a bunch of pieces (the entire red ball path)
Oh, sorry, should have had another look at the puzzle book.
In my interpretation of the rules, the required outputs are what counts and the partial solutions provided in the game book are there to help those who may need help, not to restrict those who want to think more creatively. This site says, "share your solutions to the puzzles in the book, especially if your solution uses fewer parts or solves the puzzle in an interesting way. " That last part – “or solves the puzzle in an interesting way” – is important in my opinion, so don’t spoil the spirit by making your interpretation of the rules overly rigid.
I’m not so sure about that. There are some later levels which present the same task as an earlier level but become harder by predefining different parts (e.g. the horizontal vs vertical XOR gate).
I’ll go along with that in the specific examples where a precondition makes the challenge harder. But I will not agree when a precondition is simply inelegant or leads to a wasteful solution. (Furthermore, I will probably not keep participating in a community that is policed by sticklers. This should be creative and fun, and the quote I shared from the site supports that notion.)
In this case, it does make the challenge harder - it forces you to come up with something that cycles every 3 (blue) balls since the red ball can’t be used as a 4th ball in the cycle.
Coming up with a widget that counts balls mod 3 using only blue balls is the challenge here. Scrapping the red-ball path so you can count mod 4 instead is making it much easier.
I disagree with this overall restrictive approach to the game and to the community interactivity. You guys are going to ruin the spirit of fun and you won’t increase learning or creativity. For example, in this case, rather than rejecting a solution like mine, it can be used to teach insights into modulo arithmetic. These puzzles were created by a human, not a god. They are not cast in stone. There is a better path to increasing this challenge than you guys are taking. In this specific case, one better approach is to simply pick a more challenging number than 3 blue balls + 1 red ball. I already did that and posted one alternative version of this challenge. Furthermore, on my own I solved alternate versions for many numbers of blue balls. I was inspired to do that because of exploring my first alternative version of this challenge. I get the feeling some of you do not have much experience or training in creativity and real-world inventing. Pity your enforcer attitude will spoil this community for people who might think outside the box.
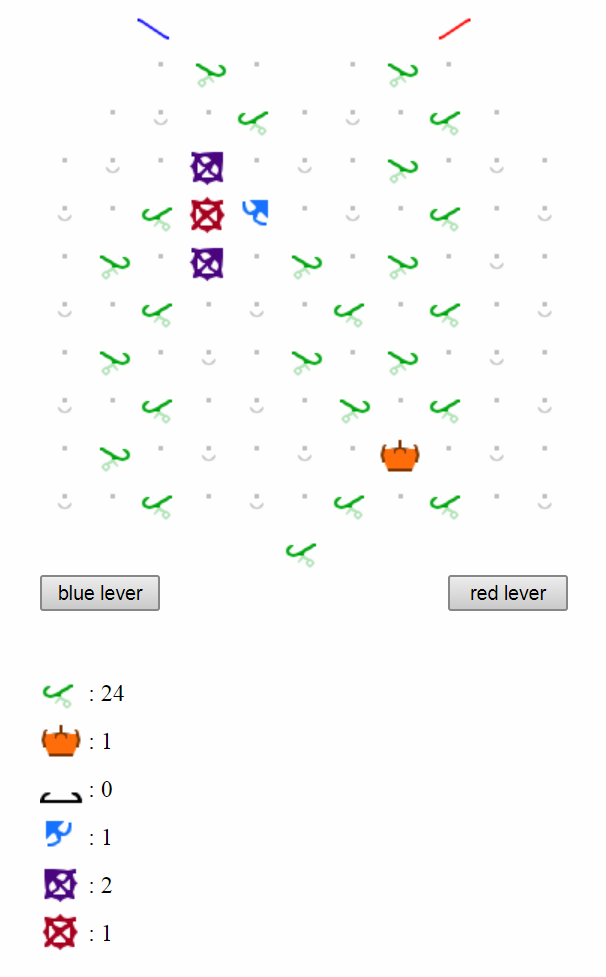
In the spirit of out of the box thinking, I have a 10-part solution:
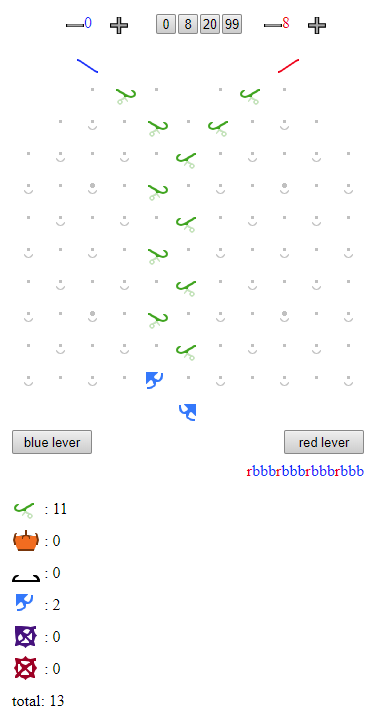
Load the blue source with BBBRBBBRBBBRBBBR, create a 10-ramp path down to somewhere on the left, and start with the blue lever.
This generalises to a 13-part solution to any puzzle where the required solution is just a fixed output pattern: alternate the pattern between red and blue sources, and use 12 ramps to feed down to a bit just above the levers.
If you really want an out of the box “solution” to any puzzle in the book: set up an empty board, with just the components specified in the required output (an interceptor or some registers or some (gear) bits) then manually place balls in the appropriate places and set (gear) bits as required. That achieves the required output to any puzzle in the book with an absolute minimum of parts.
I stand by my earlier comment: “It’s a neat way of getting the required pattern, but it doesn’t actually solve challenge #39”
It not solving puzzle #39 doesn’t mean that it’s not worth playing with and/or exploring further, just that it’s not a solution to puzzle #39. It’s like having an exam question that reads “Prove Pythagoras’ Theorem” and getting a (correct!) 5-line proof of Fermat’s Last Theorem back. It doesn’t answer the question set, but it’s far from worthless - in fact, it’d be a headline-worthy achievement and would revolutionise number theory.
I’m not condemning your layout, just saying it doesn’t actually answer the question asked.
I will really hate to see this community create a structure of overly rigid rule interpretation and self-appointed rule enforcers. That’s not ideal for encouraging learning or exploration, and it can kill the spirit of fun this community could foster. A lot of what’s important is attitude. Alternative solutions, even if they bend some of the supposed rules, can provide insights into the other solutions, including the solutions that follow the book closely. In “standing by [your] earlier comment”, you remind me of all the things I dislike about formal academia. In contrast, I hoped the Turing Tumble community would remind everyone of all the things they love about learning.
Hi Menderbug, would you like to make a variation on that one? 3b 3r and repeat… Quite a challenge for me but I assume easy for you 
Neat puzzle! It’s not too hard with “some” gears, but I wonder if there’s a way to avoid them. If we do need gears it might be cleaner to adapt Paul’s original solution instead.
Thanks, though the first sequence I got on your simulator is 3 blue 2 red, should be 3 red 
.
Yes, I am also looking for a way to program this with less expensive parts. Let’s keep each other posted on this one! Cheers.
Sorry, I accidentally generated the URL from the final state, not the initial state, so the gear bits were pointing the wrong way. I’ve updated the link in my previous post, should be fixed now.
The thing is… there is not enough parts IRL for me, as I have only got the real kickstarter here on my desk. I’ll keep looking out for another way to solve this, maybe based on this one:
If someone feels the same need as I do: generate the same pattern with less materialen, please join this conversation. Have a nice weekend!