Challenge is to create a board that generates a pseudororandom output of blue (1) and red (0) balls, thus generating a pseudorandom bit stream.
Bit stream must not repeat the pattern in less than 65,000 bits.
Use a standard width board (but can be significantly taller than the standard physical board, and use a lot more gears and gear bits than a standard set). And obviously requires a means of refilling the ball hoppers.
Solution should come with some explanation or rationale as to why it is believed to be pseudorandom and why it doesn’t repeat in less than 65,000 balls.
(This relates to several previous posts: A (almost) random pattern generator, Binary Modular Division, Instruction Stack and possibly even the I Ching ones. But this does not provide a basis for crptographically secure random number generation (unless anyone has a better solution that can??)
Solution
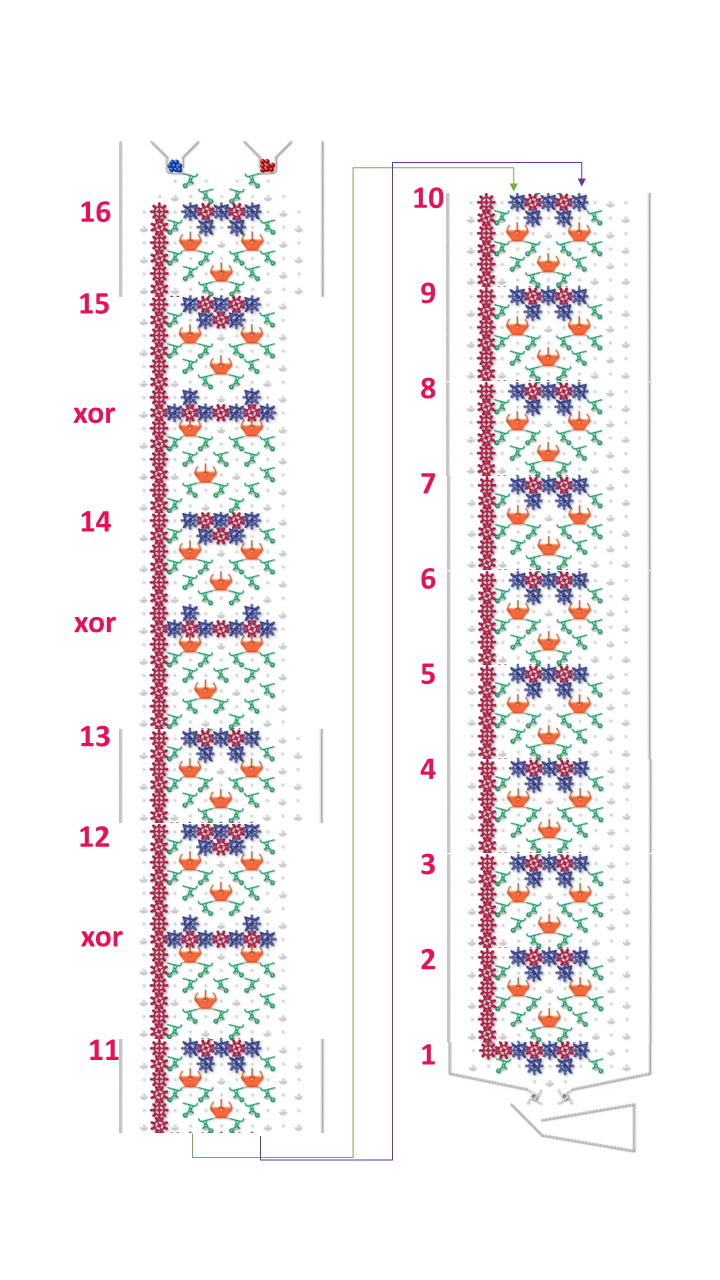
The approach is based on a Linear Feedback Shift Register, using a Galois Field and the polynomial X^16+X^14+X^13+X^11+1 . See wikipedia here for introduction.
The solution is a modified form of the Instruction Stack and the CRC4/ Binary Modular Division solutions.
That the polynomial above is primitive (leads to cycling through ((2^16)-1) steps before repeating is demonstrating by the listing of the primitive polynomial here (101101000……001).
What this means in practice is a simple shift register, where each bit takes the value the bit above it had before, with some exceptions. The XOR steps are achieved by capturing the state of bit one, and passing it up the chain. If bit 1 is 1, some of the shifts are inverted. If bit 1 is 0, they aren’t inverted.
If the bottom bit (row 1 of the shift register) is set to 1 (pointing 10 o’clock), then press blue lever to start. If bit one is set to 0 (pointing 2 o’clock) then press red lever to start. Don’t start with bits 1 to 16 as all 1s or all 0s.