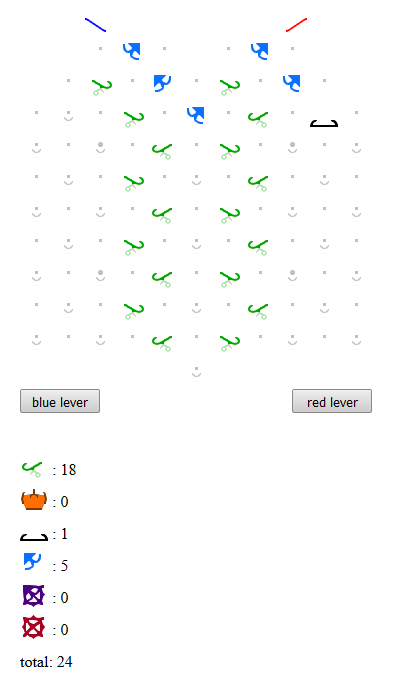
The same logic as the book solution, but by squeezing the register diagonally the last blue ball’s route joins the right path sooner, saving 3 ramps.

The same logic as the book solution, but by squeezing the register diagonally the last blue ball’s route joins the right path sooner, saving 3 ramps.
Edit: The solution below does not comply with the puzzle’s parts restriction given in the book which does not allow crossovers, so it is not a valid solution to the book’s puzzle 25. Thanks @rmsgrey for pointing this out in your post below and also for finding value in case somewants wants to optimise the number of parts given no parts restriction.
-–
@Samuel’s solution can be turned into a puzzle solution with 22 parts [edit: if one ignores the parts restriction]:
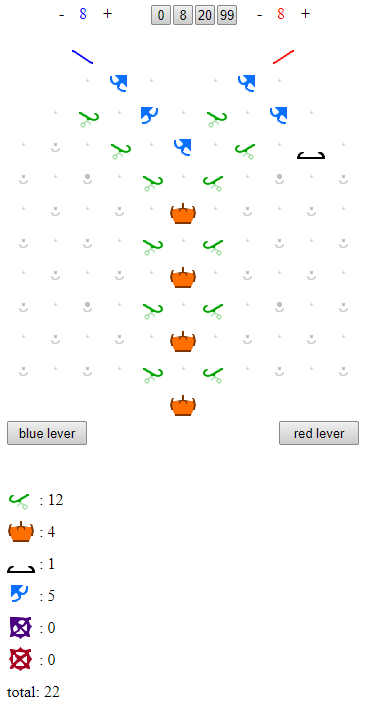
While that does reduce the part count, it also uses parts that aren’t available for this puzzle. You only have ramps, 5 bits and 1 interceptor to play with for a true solution.
Achieving the required output without following the parts restrictions, but applying some optimisation condition (such as minimising total parts) is still an interesting puzzle in its own right, but it’s not quite solving the original puzzle.