Turing Tumble Community

Puzzle 56 solution - 30 parts

Puzzle Solutions Puzzle 56
#1

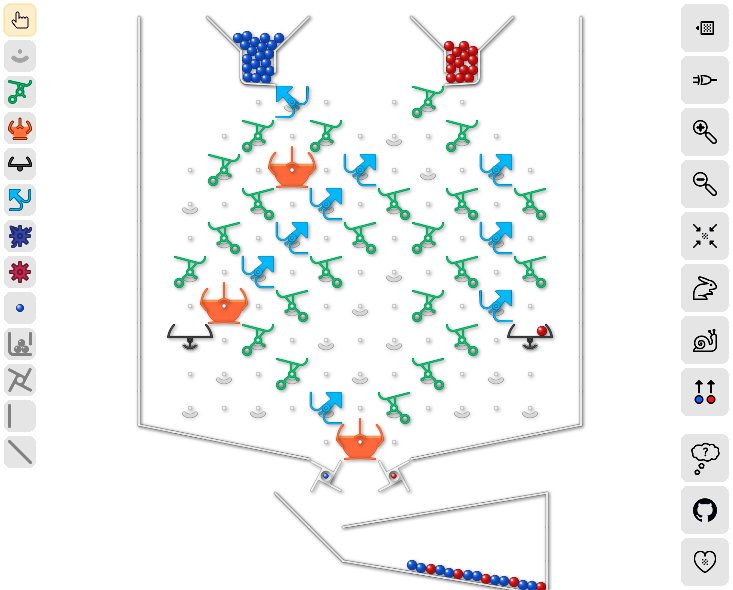
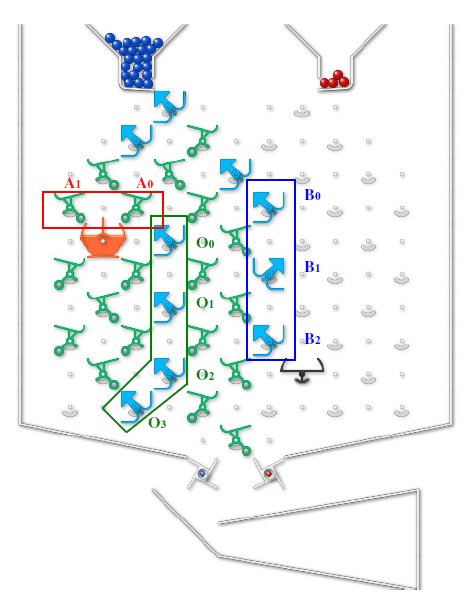
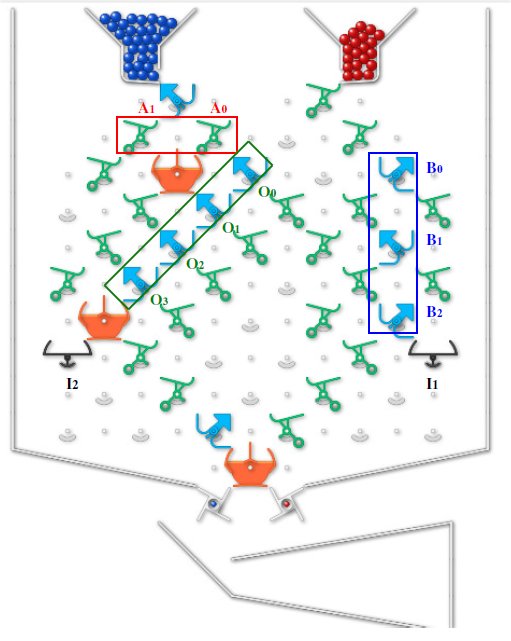
Further parts can be removed for a solution with 30 parts only:

  • Direct every second ball that enters the first bit of register A also via the second bit.

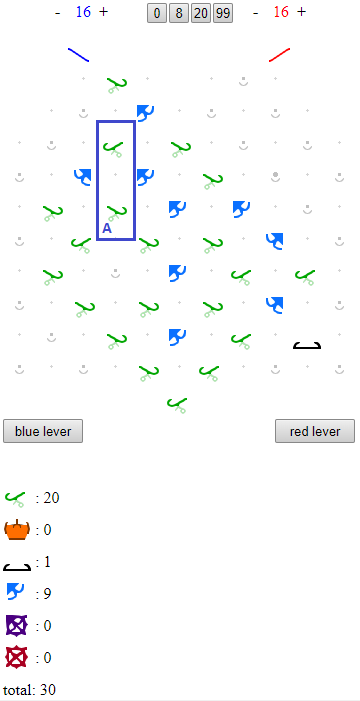
image
The bits are set up for the test with 2 x 3.
https://lodev.org/jstumble/?board=ree0flrf10reerr00eelrr1ere0llerrr1eer0lieerleel_16_16

Remark 1: The set-up does not work for 3 x 3.

Remark 2: There may still be some optimization potential regarding number of balls used, as every third ball out of four balls is running down without reaching the registers.

#2

Hello to everybody,
here is Leonardo (9y) and his grandpa NonnoGio (73y) who propose a different approach to the challenge multiplier (56), with the 3 registers A x B = O;
the attached table suggests a increment in the size of the output register (O)
from 3 to 4 bits, extending the range of possible output values (up to 15 decimal values).
56_more_bits

Looking forward to any comments,
Happy Turing-Tumble to everybody,
Gio & Leonardo

#3

Hello,
one more cntribution to the issue of the challenge 56.
We propose another approach (56_red_blue), to involve both circuits (red and blue balls)
to achieve the same result as before: A (2bits) x B (3bits) = O (4bits)
In this case the main advantage is that, at the end of the computation (as in the attached image) the original value selected for the second multiplier (B, 3bits counter) is saved in the sequence of the red-balls collected in the output chain.
Moreover the second interceptor (I2) can detect any overflow which may happen in the output buffer.
56_red_blue_end
Looking forward to any comments,
Happy Turing-Tumble to everybody,
Gio & Leonardo

#4

Hi Leonardo and Gio,

Thanks for your first posting and welcome to the community. As I got an email notification, I was more than glad to get my TT from the shelf and try your TT setup. First of all, I think it‘s a great idea to extend the multiplication for higher numbers.

I hope that I did not do any mistake in rebuilding the setup in your picture - I could not test successfully a 1x2 multiplication: With register A=1 and register B set to any number, the register O is not incrementing beyond 1 but going back to zero. This is because the lower bit of register A is directing the marble away from register O. Hope this helps.

#5

Hello Markus,
thank you very much for your comments.
You are right; there was an error in the identification of the 2-bits of the register A;
in the enclosed image you find their right position (A0-least significant-bit and A1-most significant bit);
this is the starting configuration for the multiplication A=1 x B=2
56_more_bits_c3

Moreover the left-bottom ramp must be removed (to give the way-out to the blue-ball when A1=0).

The horizontal displacement of the 2-bits register A gives more flexibility in the designof the layout and
we adopted it also in the second scheme which we proposed for the challenge 56 (using both red and blue balls),
which we include again with a correct identification of all the involved registers (A, B, O) and
interceptors (I1 for the end of the counter B, and I2 for the detection of possible overflow),
in the following post

We are now trying to address the dual problem of integer division (with underflow detection),
we’ll post our proposed approach asap.
Bye,
Leonardo & Gio

#6

Here is the second scheme for the solution to challenge 56
56_red_blue_start_S

2 Likes