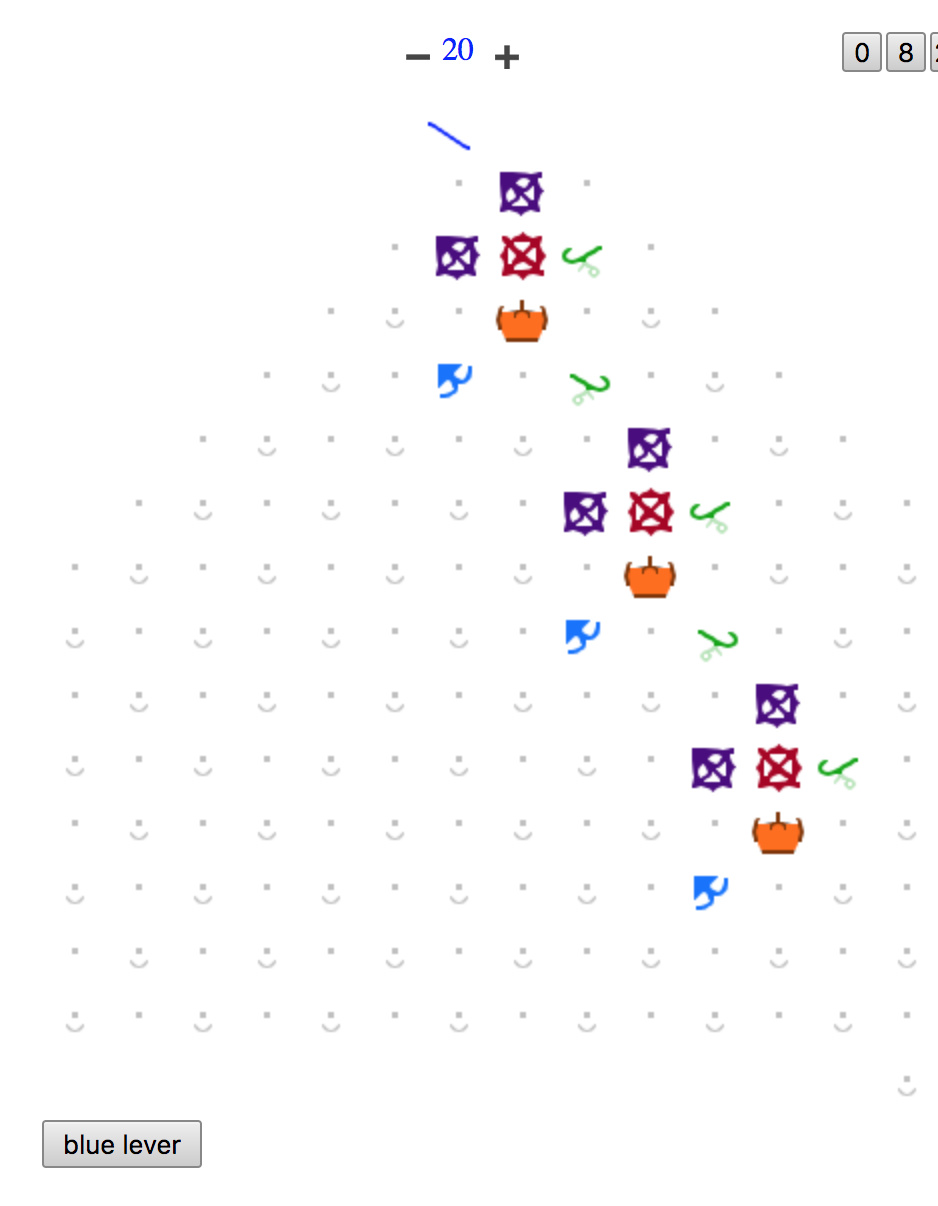
This is a theoretical challenge. Finding a solution and explaining it will naturally be harder (and different) than typical puzzles.
Suppose that…
- In addition to blue bits, we have red bits. The only difference is color and only to make it easier to distinguish these special bits from any regular bits that may be added.
- There is one ball drop instead of two at a fixed location on the board.
- The board is infinite in extent around the ball drop. (The upper portion may be ignored.)
- An infinite number of flippers are available. When a ball lands on one, it is removed from the board and a new ball is released from the ball drop.
The challenge: Place an infinite number of red bits along with any number of other components (except intercepters) such that…
- Each red bit is in its own column. That is, no red bit is directly vertically above another red bit.
- Each red bit is flipped exactly once.
- Each red bit is flipped within a finite amount of time from the first ball dropping.
- Each ball flips at most one red bit. (Edited this in just now.)
There is no requirement that these red bits be at the same horizontal level. I expect they will be along diagonal lines in some way.
I don’t (yet) have a solution for this. Good luck!