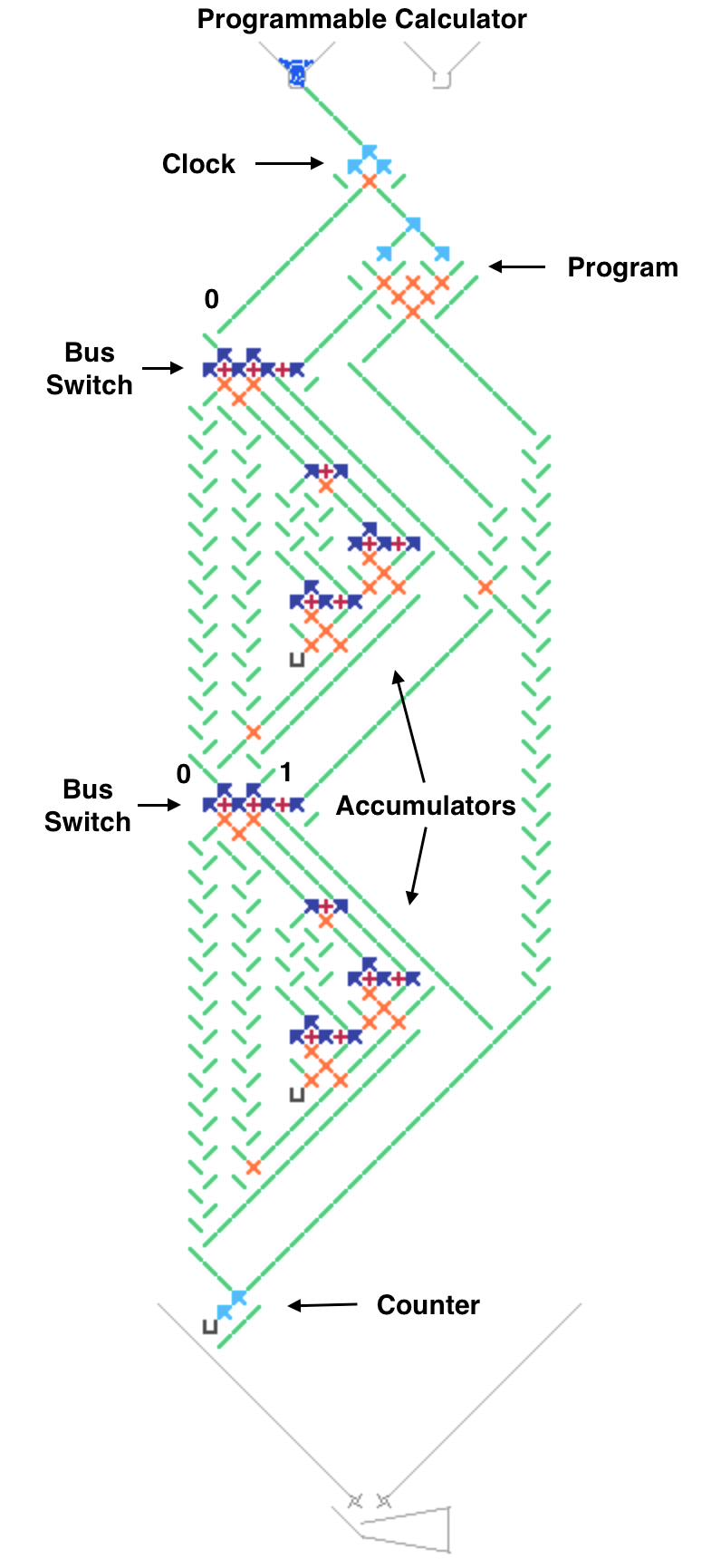
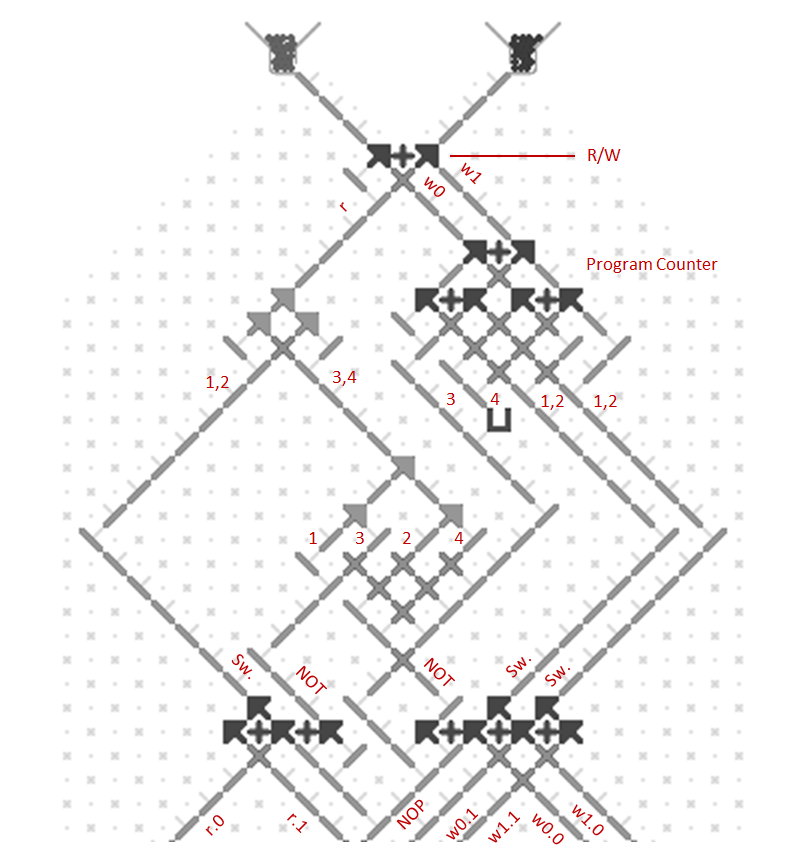
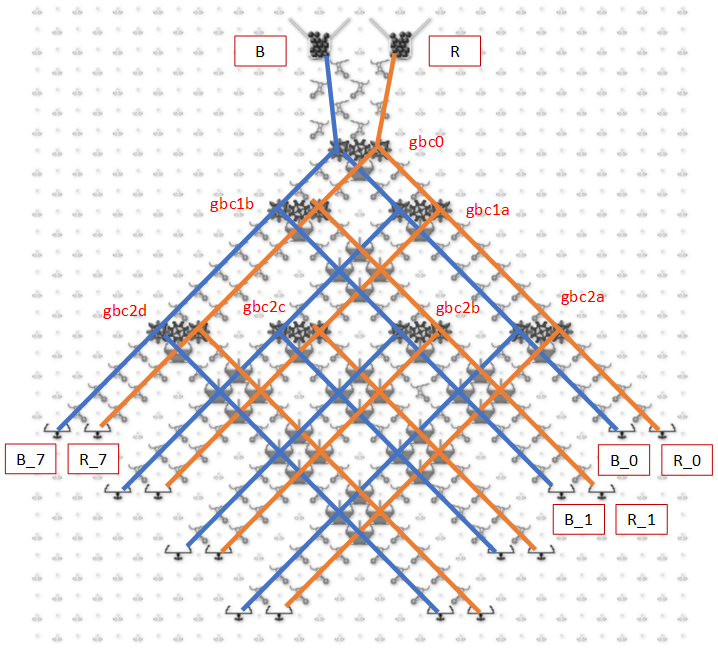
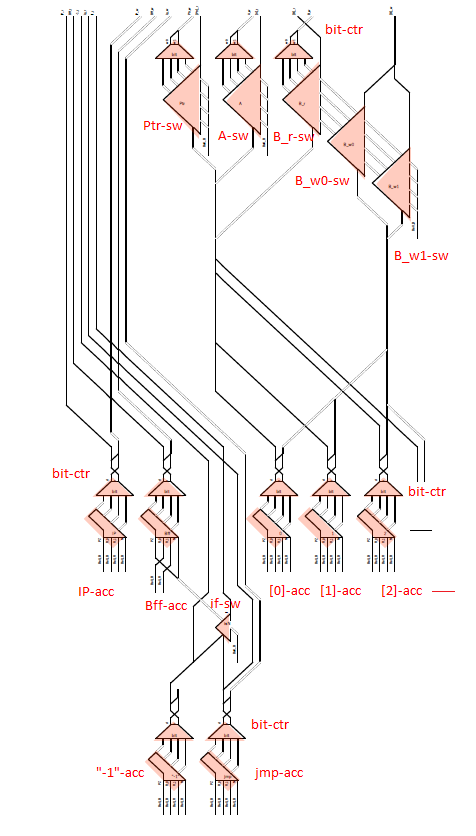
Here’s an approach for building Turing Tumble machines using read/write registers with a serial data bus. Each register stores a binary number and can support reading, writing, addition and other operations. Two parallel ball paths (0 and 1) are used as a serial bus for sending binary numbers between registers one bit at a time. Each register has 0 and 1 paths for both input and output. A simplified Babbage Difference Engine using some Digi-Comp II ideas is shown as an example.
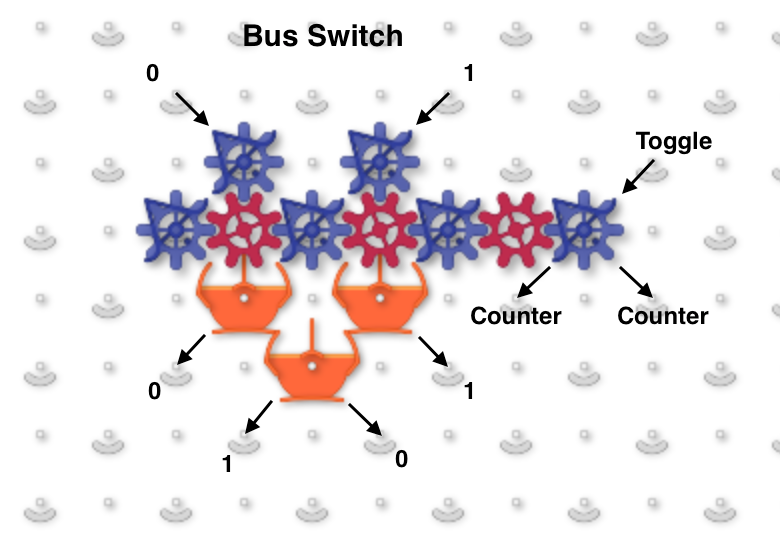
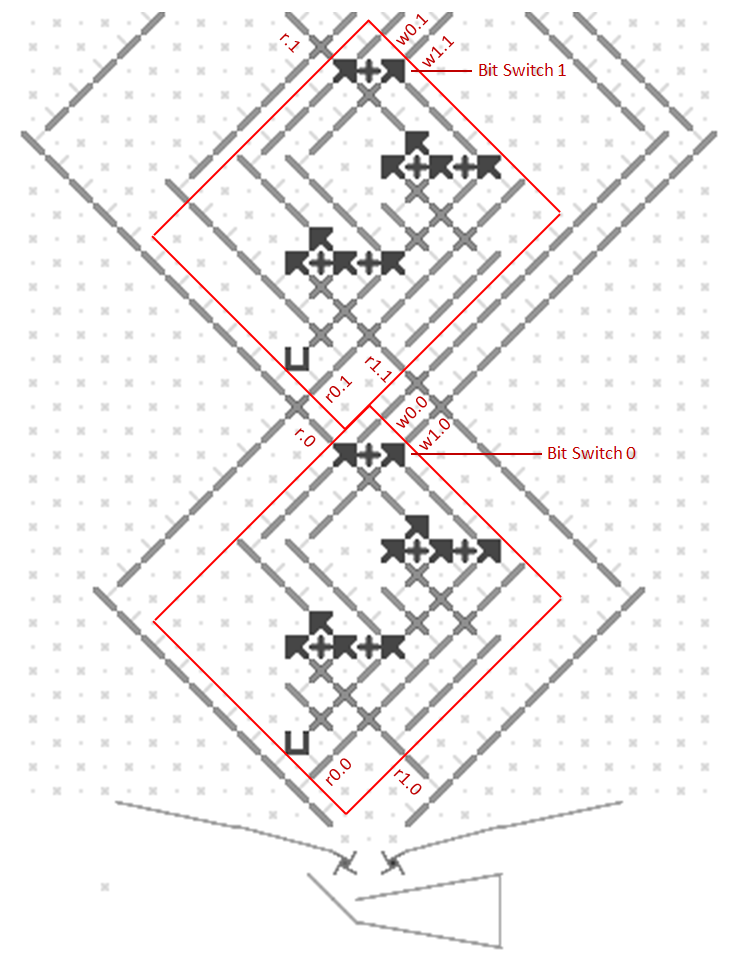
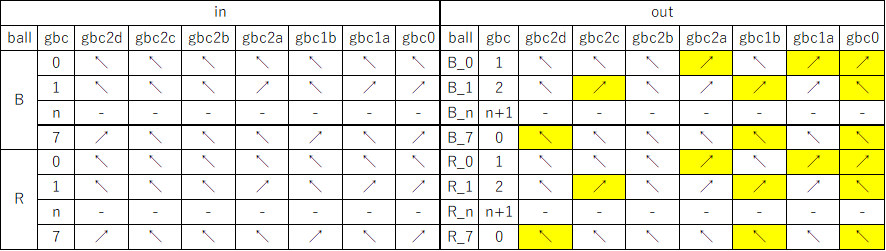
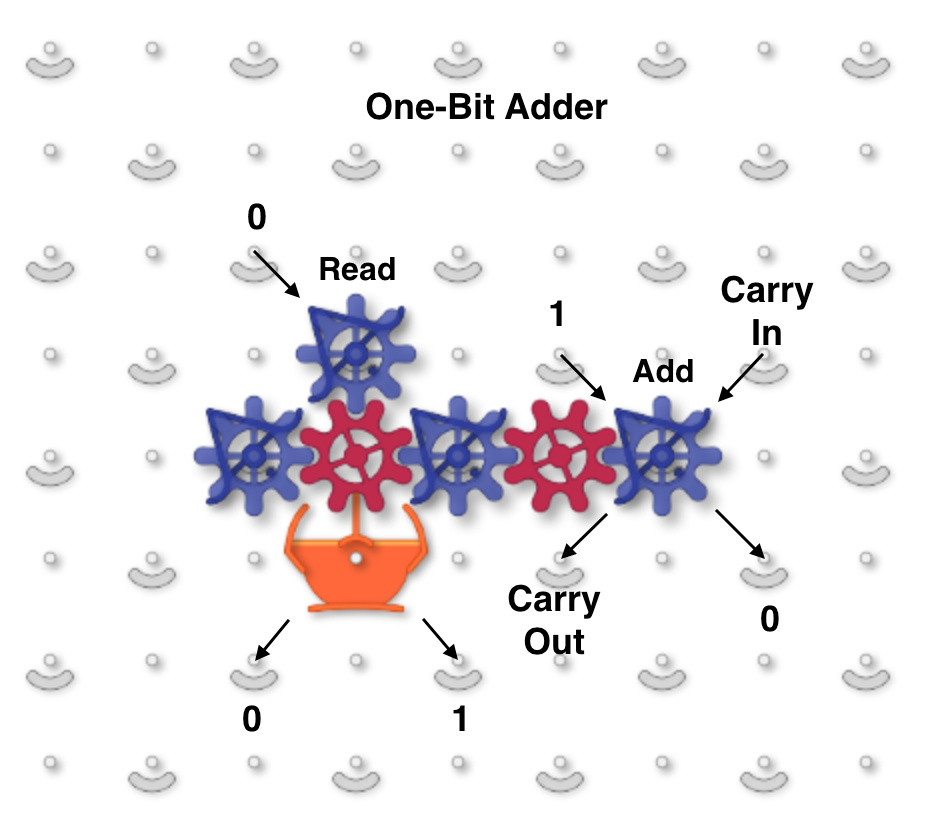
This image shows a one-bit read/write adder with gear bits set to a 0 value. Instead of using ramps for read-only registers and bit parts for write-only registers it combines the features of both using gear bits. An input 0 ball goes through two gear bits on the left and reads the current value to the output 0 or 1 path without changing it. A 1 ball toggles the rightmost gear bit to add to the value and handle carry in and out.
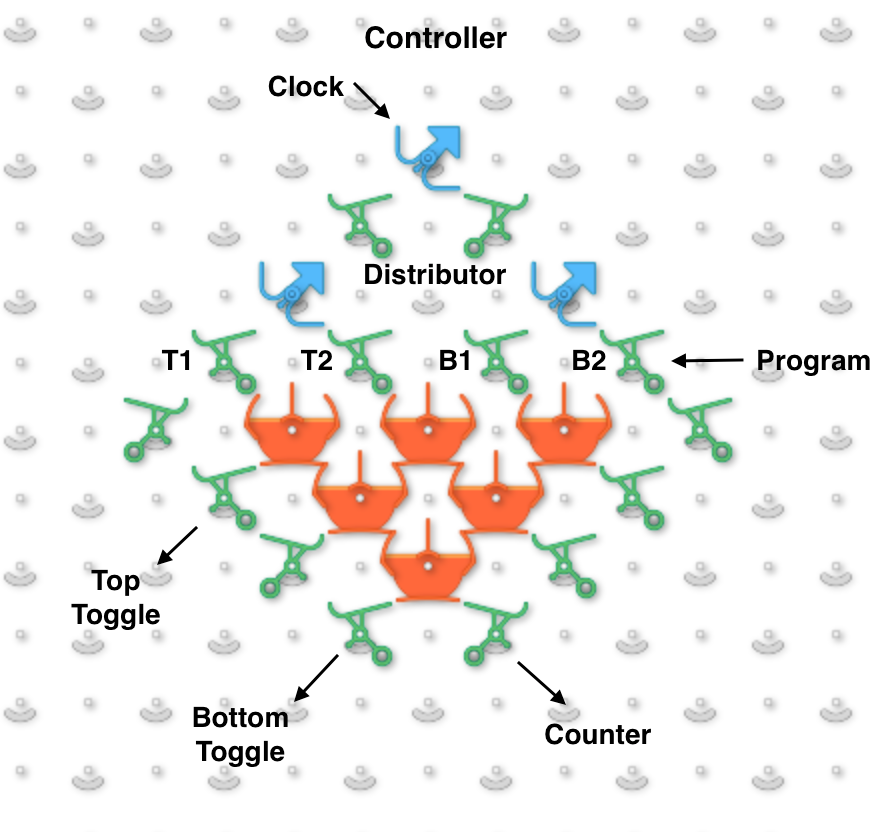
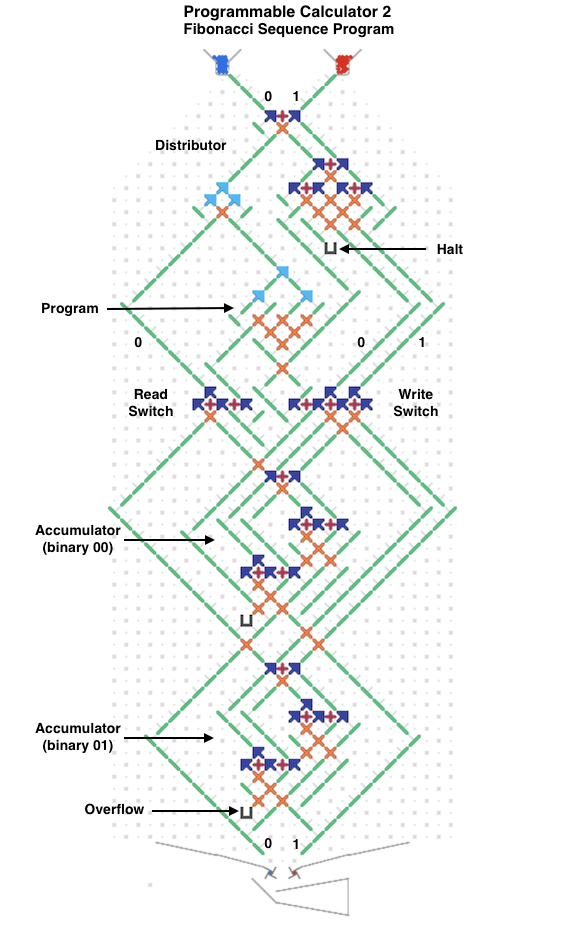
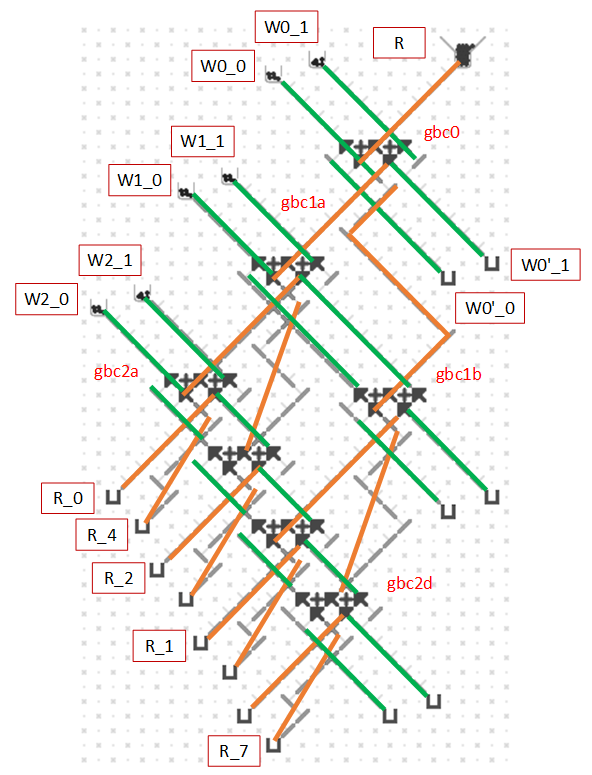
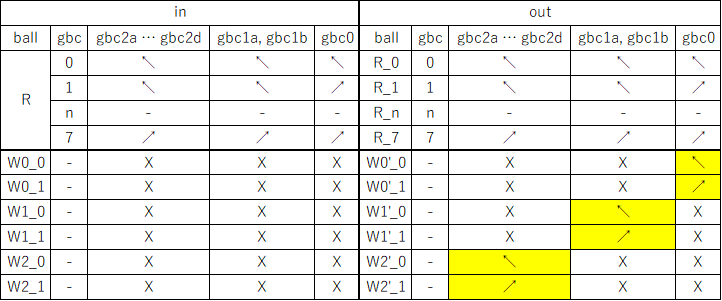
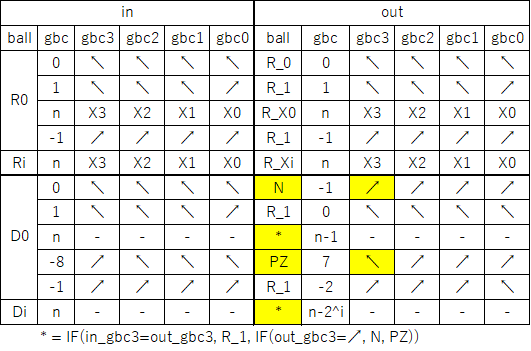
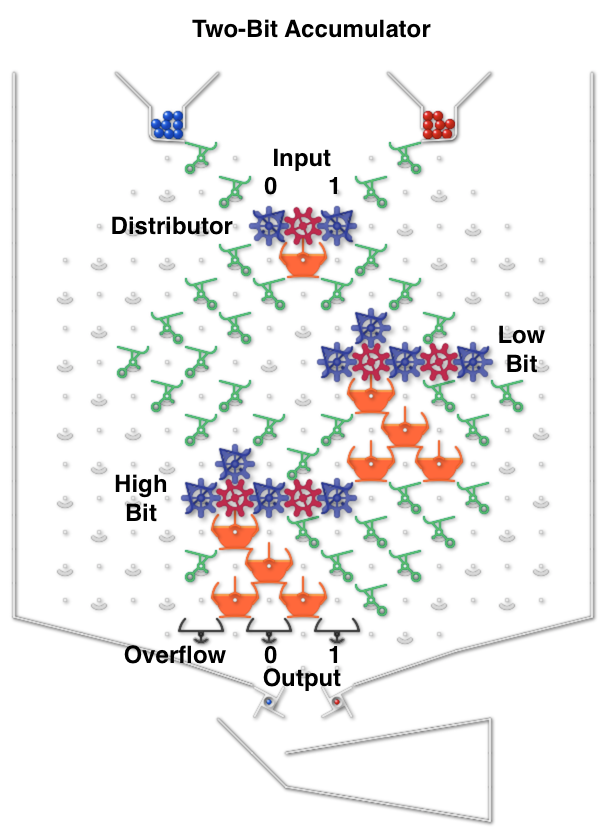
The next image and simulator link show a two-bit read/write “accumulator” register containing two adders. Each accumulator has a “distributor” that routes input balls to each adder bit sequentially. Binary two-bit numbers are sent serially as two balls with each ball in either the 0 (left) or 1 (right) path. An all-zero input number will read the current value to the serial output 0 and 1 paths without changing it. Any 1 balls add to the accumulator and handle carry and overflow.
To run, use the 0 (blue) and 1 (red) levers to input two-bit binary numbers and observe the arithmetic operations. For example, entering a red and then a blue ball for binary “10” will add decimal 2. The output balls in this example go to interceptors but could go to another accumulator. For example, a “00” number could be routed through two of these accumulators stacked vertically to read the first one and add its value to the second.
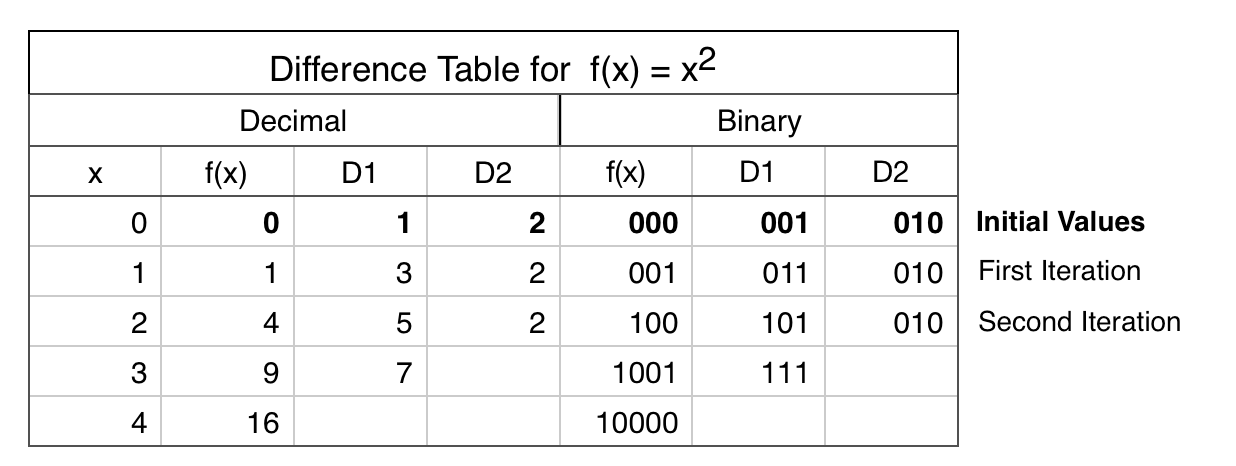
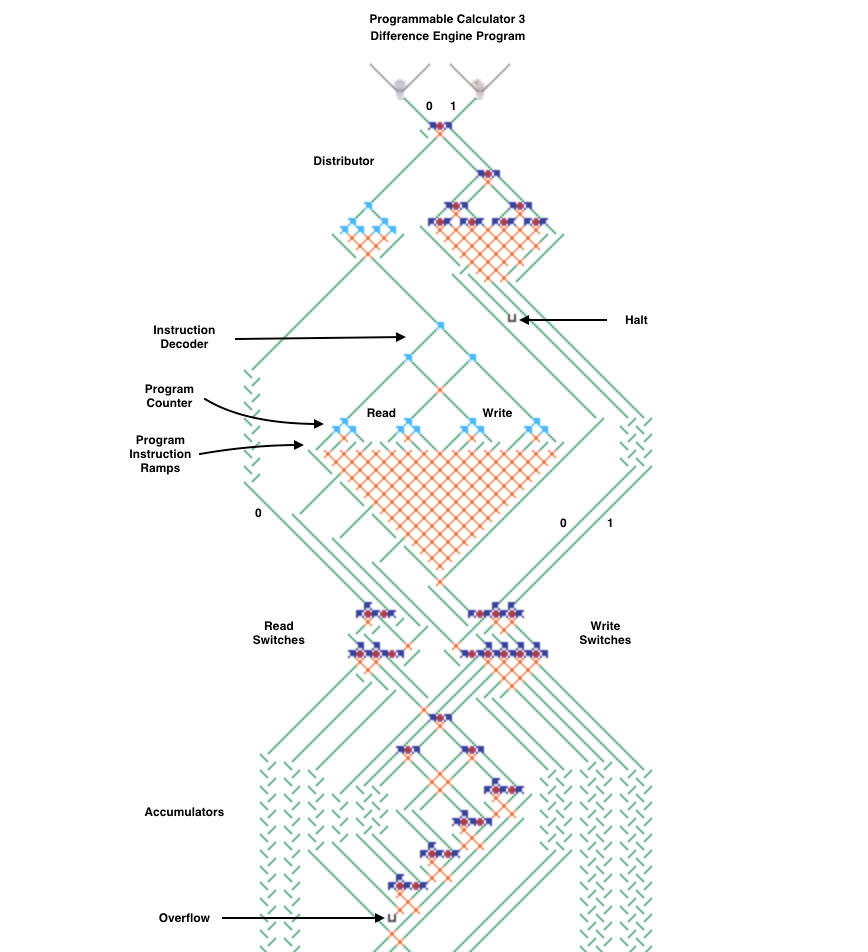
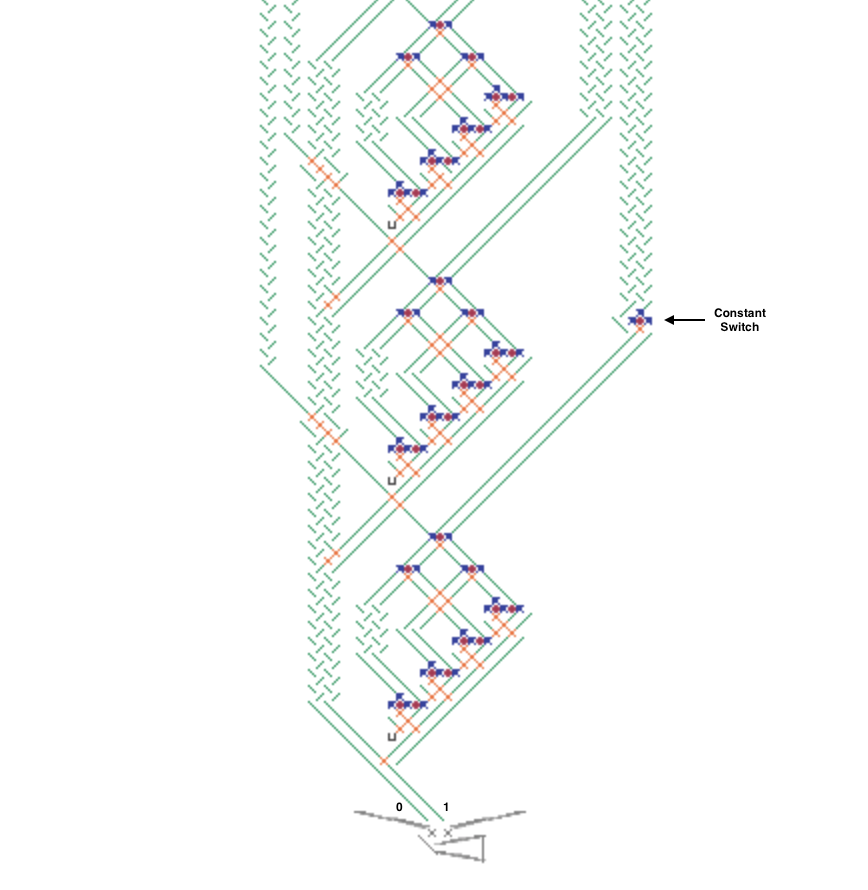
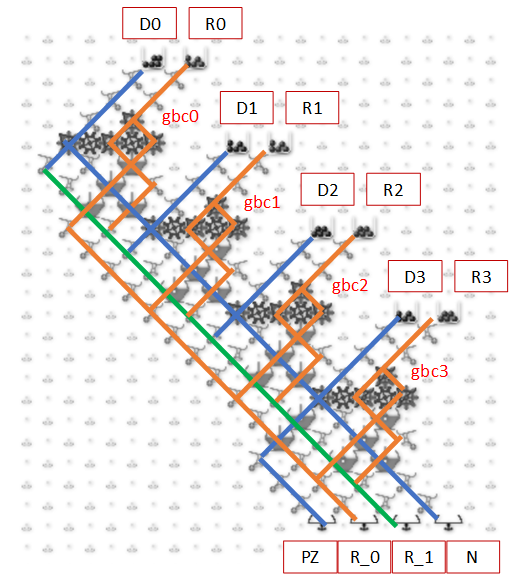
The next image and simulator link show a simplified Difference Engine using three four-bit read/write accumulators. It evaluates quadratic polynomials using only addition. Using more stacked accumulators will calculate higher order polynomials without using any more balls. The number of bits per accumulator can be increased. To match Babbage’s precision would require eight 64-bit accumulators.
The accumulator three low bits represent values from 0 to 7 (binary 000 to 111). The high bit clears every second number to all zeros to read the accumulator below it and add to the one below that. These clear bits must be initialized to alternating directions for each accumulator which alternates between adding even numbered accumulators to odd numbered ones and vice versa. Each even/odd loop iteration repeats two operations: add the D1 accumulator value to the f(x) one, then add D2 to D1.
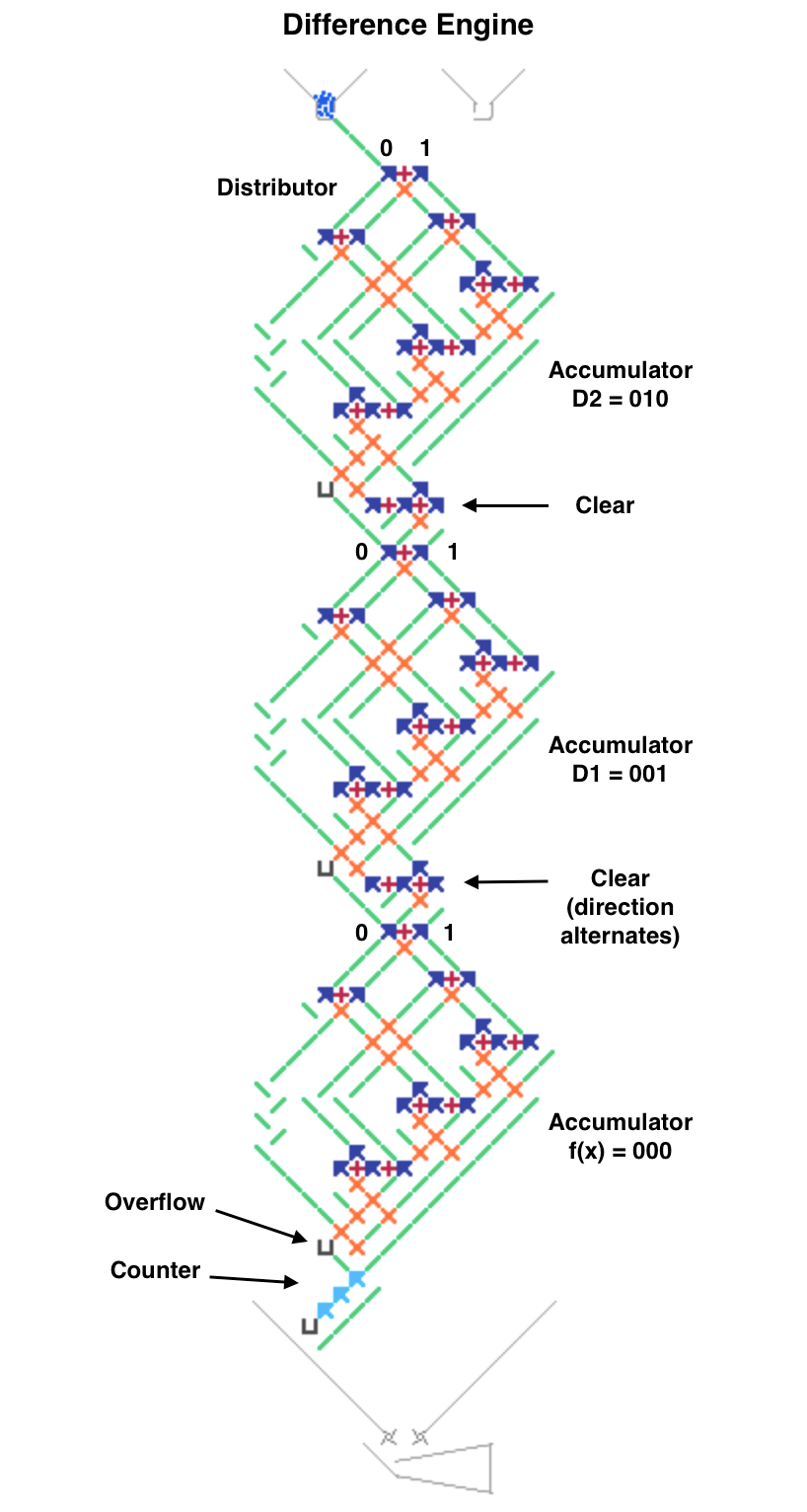
To calculate a polynomial function f(x) such as “x squared” make a difference table where each D1 and D2 entry is the difference of the two numbers to its left. Both decimal and binary values are shown in the table below for clarity. Enter the top row initial values 0, 1, 2 (binary 000, 001, 010) in the accumulators from bottom to top (already done for this example in the image and simulator link). Calculating initial values is more complicated for higher order polynomials using more accumulators.
To run, press the blue lever. Each full even/odd eight-ball iteration calculates the next row in the difference table with the f(x) results 0, 1, 4 (binary 000, 001, 100) in the f(x) accumulator until it overflows before reaching 9. The counter at the bottom pauses after each iteration to view the result (use the blue lever to continue).