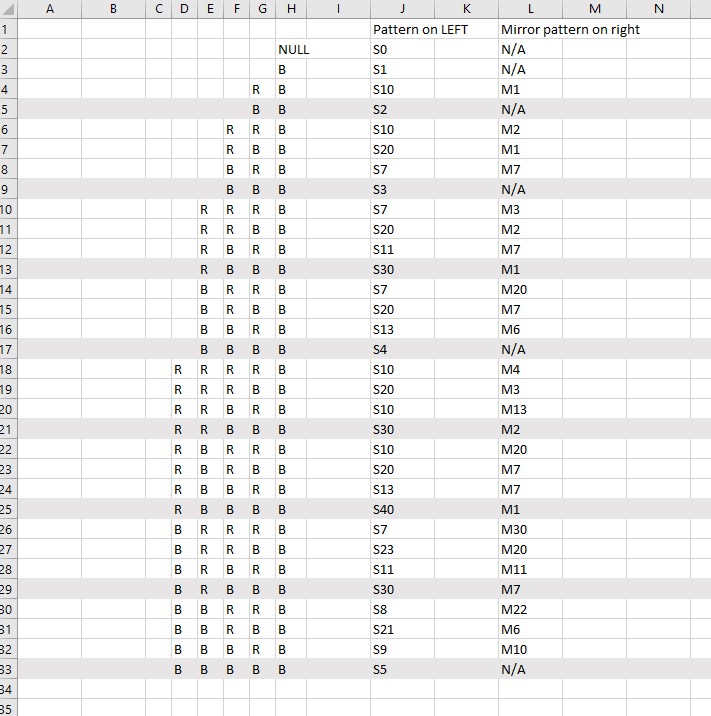
Basic idea is to “Create a configurable board that can create any pattern”.
Challenge 1: any one ball pattern ( trivial)
Challenge 2: any one or two ball pattern.
Challenge 3 : any one, two or three ball pattern.
Main challenge- how many balls is the maximum for this genre of challenge.
Fine print: standard board size, limit of number of pieces in the physical set, ball hoppers to be full (20), pattern creation has to terminate with an interceptor. Board has same pieces on it for the whole challenge. Configuration of the board to create a specific desired pattern consists of moving bits and gear bits. Ramps cannot be turned round. By configuring the bits, produce the different patterns with same board. Example: challenge three must be capable of being configured to give r, b, br, bb,rb, rr, rrr, rrb, rbr, rbb, brr, brb, bbr, bbb, - depending on how the bits are set up in advance.
:
I have boards for both challenge 2 and 3 but I really think that my solutions are too complicated for their respective tasks.
Challenge 2
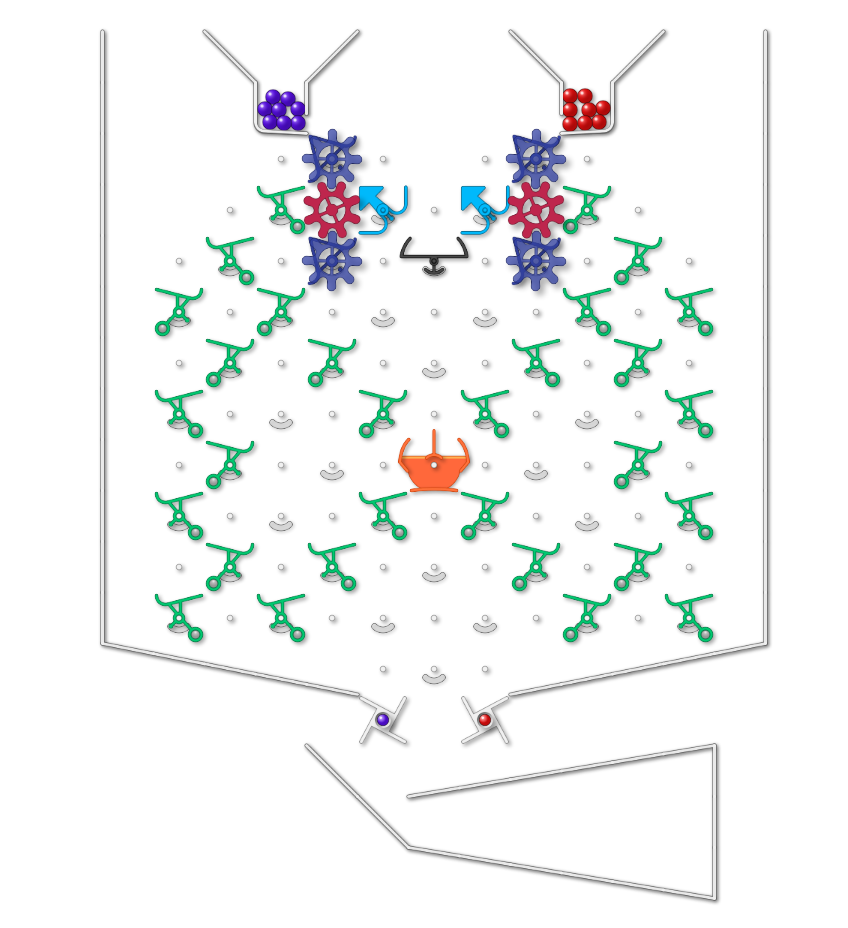
Challenge 3
Very nice @Florentin.
Your solution to challenge 3 is tantalising as it can also do all but 2 of the 16 possible 4 ball patterns too!
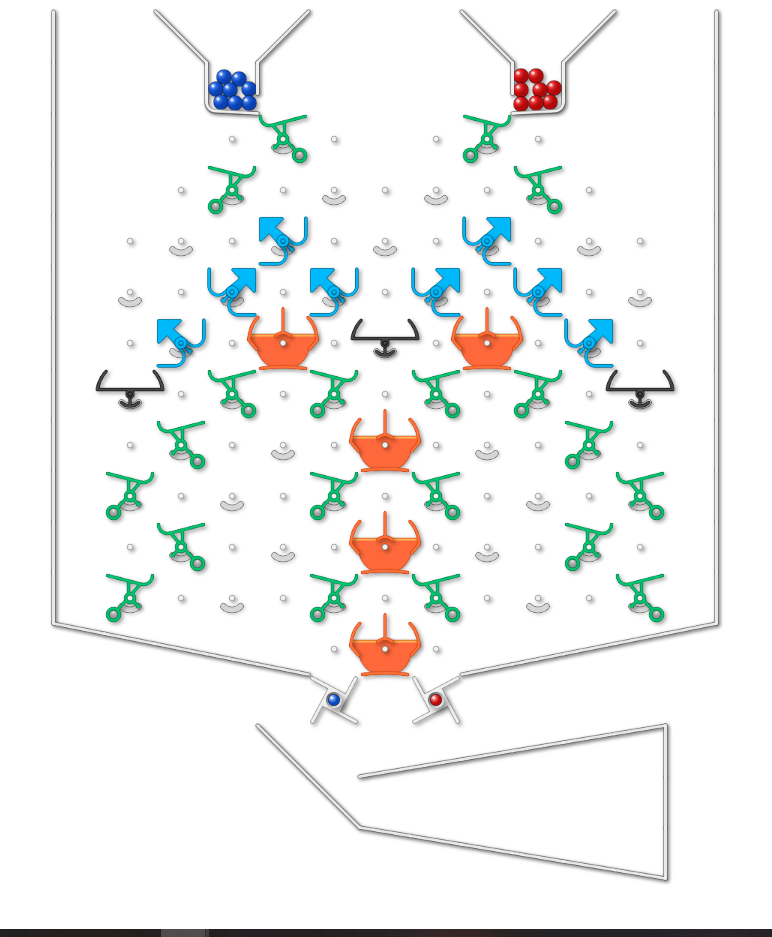
I believe I have a solution for Challenge 4. It can definately do some of the harder ones like bbbb, rbrb, brrb, and brbb.
(I can also see a way that just might allow a solution to Challenge 5, but I am back at work now, so may be a while coming)
Challenge 4 - picture of solution
This text will be hidden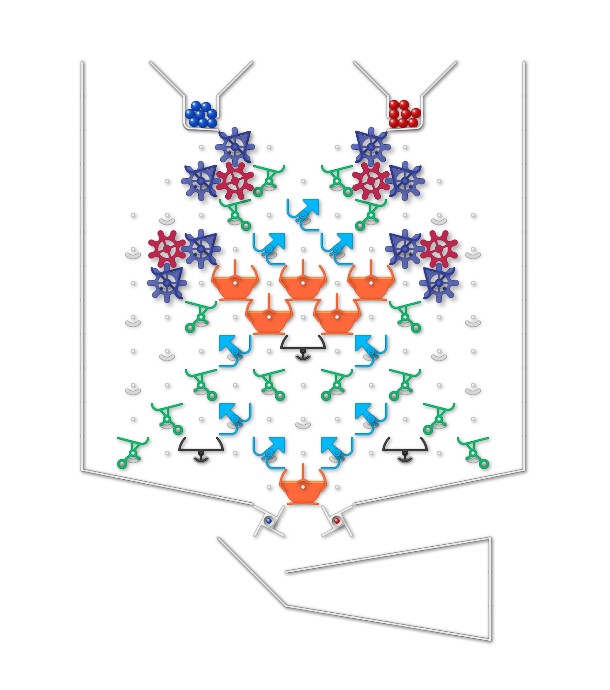
Hi @florentin - here is a solution for Challenge 5 (pretty certain, unless I’ve made a mistake somewhere - there is a LOT of ways to arrange this board). I plan to post an explanation and “proof” that its a solution in next couple of weeks.
Challenge 5 - Solution
Solution to Challenge 5. Explanation to follow .
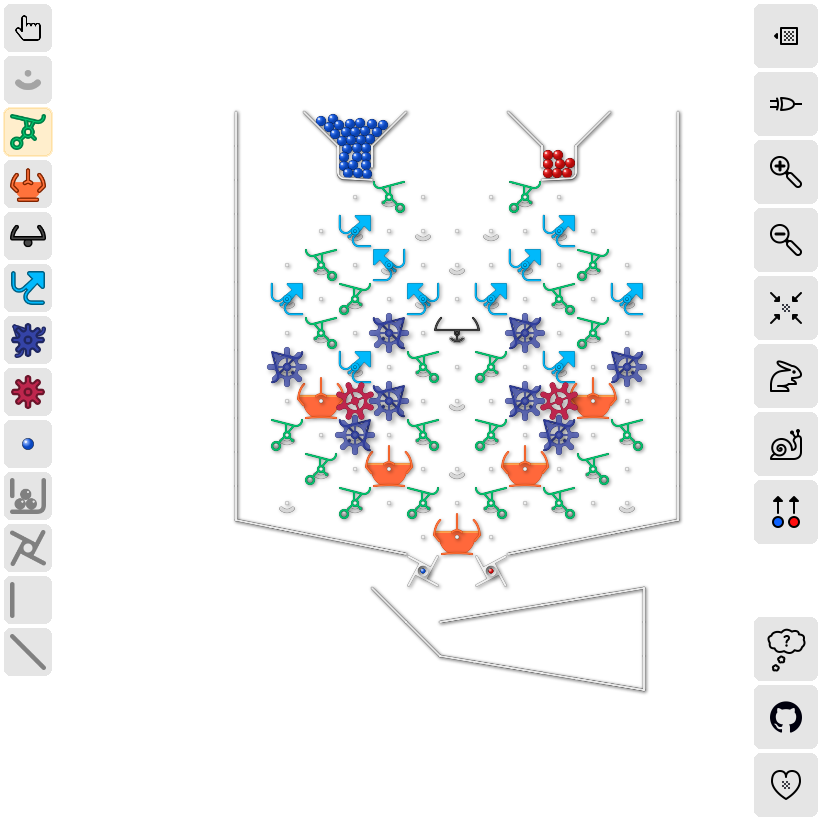
Explanation and demonstration of solution to challenge 5
Solution - with explanation
Explanation of solution to “universal pattern generator” for up to and including 5 balls
(Any colour, standard board, supplied pieces)
Solution is symmetrical, so we only need to show all patterns where the first ball is blue (all patterns where first ball is red are mirror images).

Proof starts by considering a “half board” (see figure below – which also defines a numbering system for the bits and gear bits).
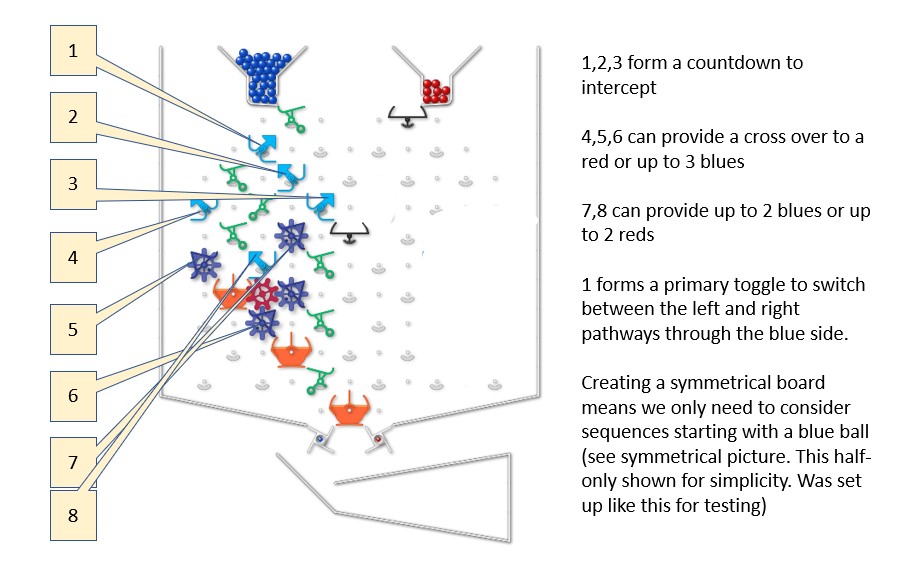
Depending on how the 8 bits are set, the first blue ball can either:
- Be intercepted
- Release another blue ball
- Release a red ball.
Each configuration on this “half board” can be left to run until a blue is intercepted, a red is triggered (and in the half board, immediately intercepted).
If the end is release of a red ball, the half-board is left in particular configuration (having passed the action to the red side). If the red side passes the action back (after release of either 1, 2, 3 etc red balls), the action of returning to the blue side is simulated by pressing the blue lever a second time. In some cases a 3rd press is needed (to create a pattern like BRBRB, or to pass back from red to blue and intercept immediately.
The proof has two parts – identifying relevant configurations of the half board (and how they behave), then stringing together these with their mirror image equivalents to create any required pattern.
Sn is the nth configuration below. Mn is the mirror equivalent on the red side.
Configurations of a half board:
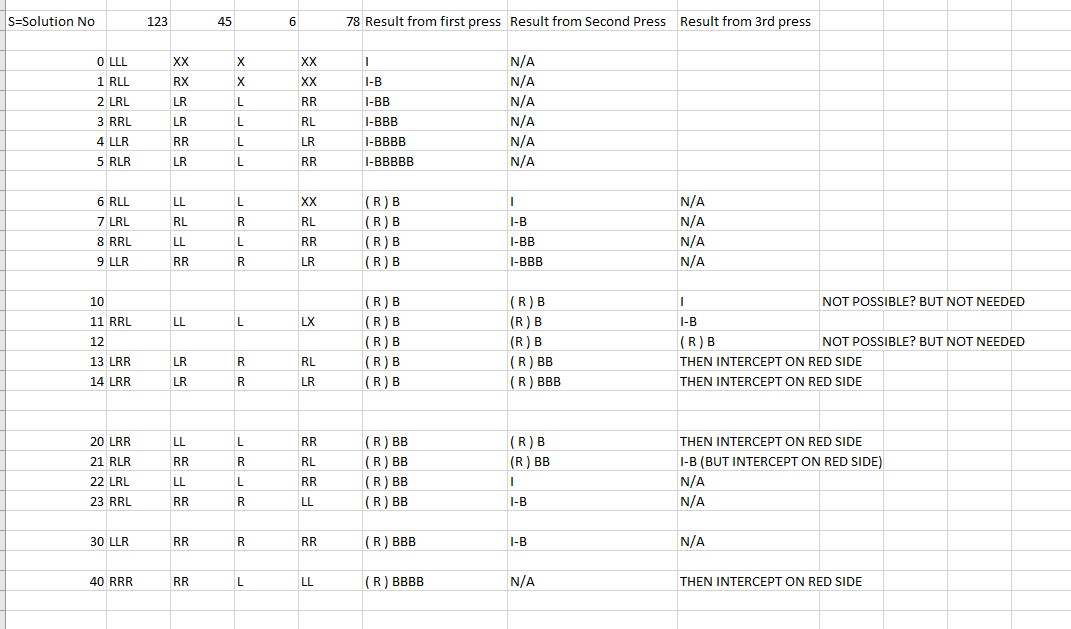
Combinations of half-board solutions: