The problem with asking to explain what each individual component in a solution does is that it’s a bit like asking someone to explain how to use a calculator by telling you what each electronic component does.
I can try to talk you through the very first problem. You start with the board with 6 green “ramps” and 8 blue balls loaded into the top:
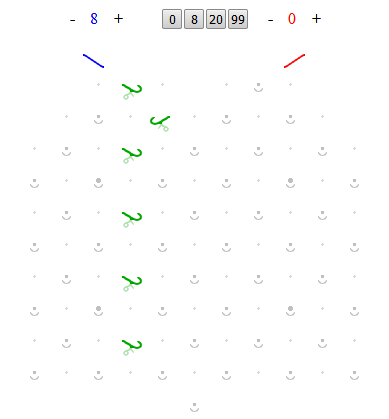
You are allowed to add up to 4 more ramps to complete your solution, and then, by triggering a blue ball’s release and then letting the system run until everything stops moving again, you need to get all 8 blue balls into the output tray at the bottom.
Ramps face either to the right or to the left, take a ball dropped onto them from above-right or above-left, and drop it onto the next component down in the direction they’re facing. With the starting setup, if you release a blue ball, it’ll come down off the blue input path onto the top ramp, roll down to the right onto the next ramp, where it’ll roll down to the left onto the third ramp, which will drop it into open space since there isn’t a component diagonally below and to the right of that third ramp to catch the ball. That’s a problem. Physically, sometimes the balls will still do what you want after dropping through one or more empty spaces, but, even if they land on a suitable component further down the board, they tend to bounce wildly and unpredictably, so there’s an additional rule: except at the bottom of the board, you always have to drop the ball directly onto another component, never into an empty space.
When a ball reaches the bottom of the board, if it’s on the left side, it will trigger the release of a blue ball; on the right, it will release a red ball. In both cases, it’ll only actually release a ball if there’s one waiting at the top.
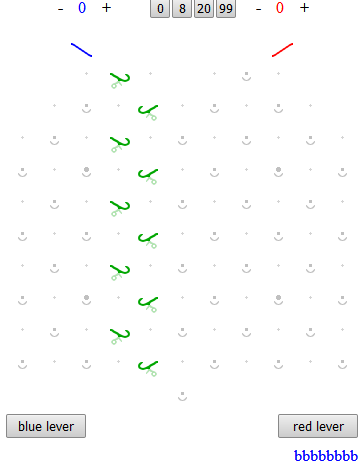
So the big-picture here is to complete a path so that when a blue ball is released, it rolls safely from component to component all the way down to the bottom, ending up on the left side to release a new blue ball. To do that, simply add the 4 new ramps to give:
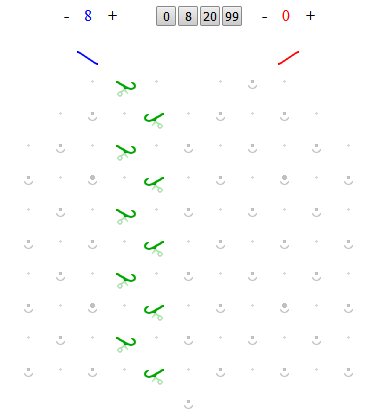
Now, counting from the top, the first, third, fifth, seventh and ninth ramps will drop the ball down and to the right onto the next ramp, while the even-numbered ramps will drop the ball down and to the left onto the next ramp, with the exception of the tenth ramp, which will drop the ball into the left output, where it triggers a new blue ball to be released then gets added to the output rack. The next blue ball will follow the same path, dropping from ramp to ramp and triggering a third blue ball to be released. The eighth blue ball will attempt to trigger a ninth, but since there isn’t one, no ninth ball will be released, and the eighth ball will just roll down to the output rack leaving a row of 8 blues in the output:
Puzzle 21 asks to load any number of blue balls between 1 and 15 (inclusive) into the input, and then count how many there are. The puzzle leaves out the 5 left-facing ramps, but figuring out where to put them should be automatic after completing the first 20 puzzles, so the solution is:

The blue components are “bits” and can point either left or right. When a ball drops onto one, the bit changes to the other direction, and sends the ball in that new direction. So when the first blue ball is released, it will fall onto the top bit, which will switch from left to right, and the ball will drop out to the right. From there, it will drop from ramp to ramp, alternating right and left, until it reaches the bottom on the left and releases a new blue ball.
The second blue ball will drop onto the now right-facing top bit, and switch it back to the left, with the ball also dropping to the left, where a ramp drops it onto the second bit, which will switch from left to right, dropping the ball to the right, where it will zig-zag down the ramps to release the third blue ball. That will switch the top bit from left to right, and then zig-zag down the ramps on the right, giving:

Of the 11 blue balls I started with, 3 are in the output, 1 is just starting its journey, and 7 are waiting in the input hopper. Meanwhile, the top two bits have been switched, so the four bits that (reading from the top) started LLLL are now RRLL.
The fourth ball will switch the top bit to the left, getting fed back into the second bit, which will also switch to the left, feeding the ball into the third bit, which will switch to the right, after which the ball will zigzag to the bottom. The new pattern will be LLRL. The top two bits are now back how they started, so the next three balls, balls 5, 6 and 7, will follow the same paths as balls 1, 2 and 3, with the only difference being that the third bit is pointing right throughout rather than left.
After ball 7, with the pattern RRRL, the eighth ball will, like the fourth, reach the third bit after setting the first two to the left. Unlike with ball 4, the third bit is currently to the right, so switches to the left, and ball 8 drops to the left and then off the ramp there to the bottom bit, which is set to the right, giving the pattern LLLR. For the remaining balls (9, 10 and 11), the same paths as balls 1, 2 and 3 are again followed, going through patterns RLLR, LRLR and finally RRLR:
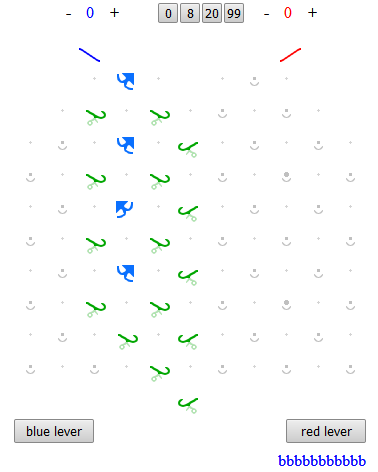
The only question then is how to interpret that board-state as a number. The key is binary arithmetic: interpreting R as 1 and L as 0 and reading from the bottom, looking at the state of the board as each new ball is released, it goes: 0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, 1001, 1010, 1011 - the binary representations of numbers zero to eleven in order. If the balls hadn’t run out, it would have continued counting in binary all the way up to fifteen (1111), then the sixteenth ball would have reset the counter to zero because there isn’t a fifth bit there to allow five-bit numbers to be represented.
Binary numbers? Normally we work in the decimal, or base-10 system, where the rightmost digit (ignoring fractions) is the units digit, or ones digit, the next digit over is the tens digit, followed by hundreds digit, thousands digit, ten-thousands digit, hundred-thousands digit, millions digit, and so on. The value of a number in this system is what you get when you multiply the value of the digit in a given position by the value of that position for every digit in the number, and then add those products together. For example, 527 is five hundreds, plus two tens, plus seven ones, or five hundred plus twenty plus seven or five hundred and twenty seven. In this system, each position is worth ten times as much as the position to its right. In the binary system, rather than going up in tens, you go up in twos - each position is worth twice as much as the position to the right, and you only need two digits - 0 and 1 - to represent any number. For example, 1011 is (reading from right to left) one one, plus one two, plus zero fours, plus one eight, or one plus two plus eight, or eleven.
You can use a similar (but subtly different) layout to count down instead of up, and, with a bit of thought, you can combine those two layouts so that you have two numbers, each represented by a column of bits, and count one down while the other counts up until the one counting down reaches 0, and stop the machine there (using an “interceptor” piece that just catches a ball and stops the machine without it needing to run out of balls) in order to add the two numbers together.
Meanwhile, have you checked out the education resource page - https://edu.turingtumble.com/ - the educator guide - https://www.turingtumble.com/edu/Turing%20Tumble%20Educator%20Guide%201_0.pdf - offers advice, background information and guidance for using the first 30 puzzles in a classroom, which might shed more light on matters.