Continuing the discussion from My 1st puzzle  :
:
I am not all the way through the book yet, so I do not know how to use the gear pieces yet and I was wondering if anybody had created a solution to this puzzle without the gears and if it is possible. Thanks!
@TTM180 I cannot think of a way for that puzzle to be done without the gears. When a ball passes through one gear bit, it changes the direction of the second gear bit, adding in the logic. I’m excited for you to get to the puzzles with the gears. They are going to blow your mind!
@Ollieryan Am I right that your puzzle can’t be done without gears?
I’m excited too! Thanks!
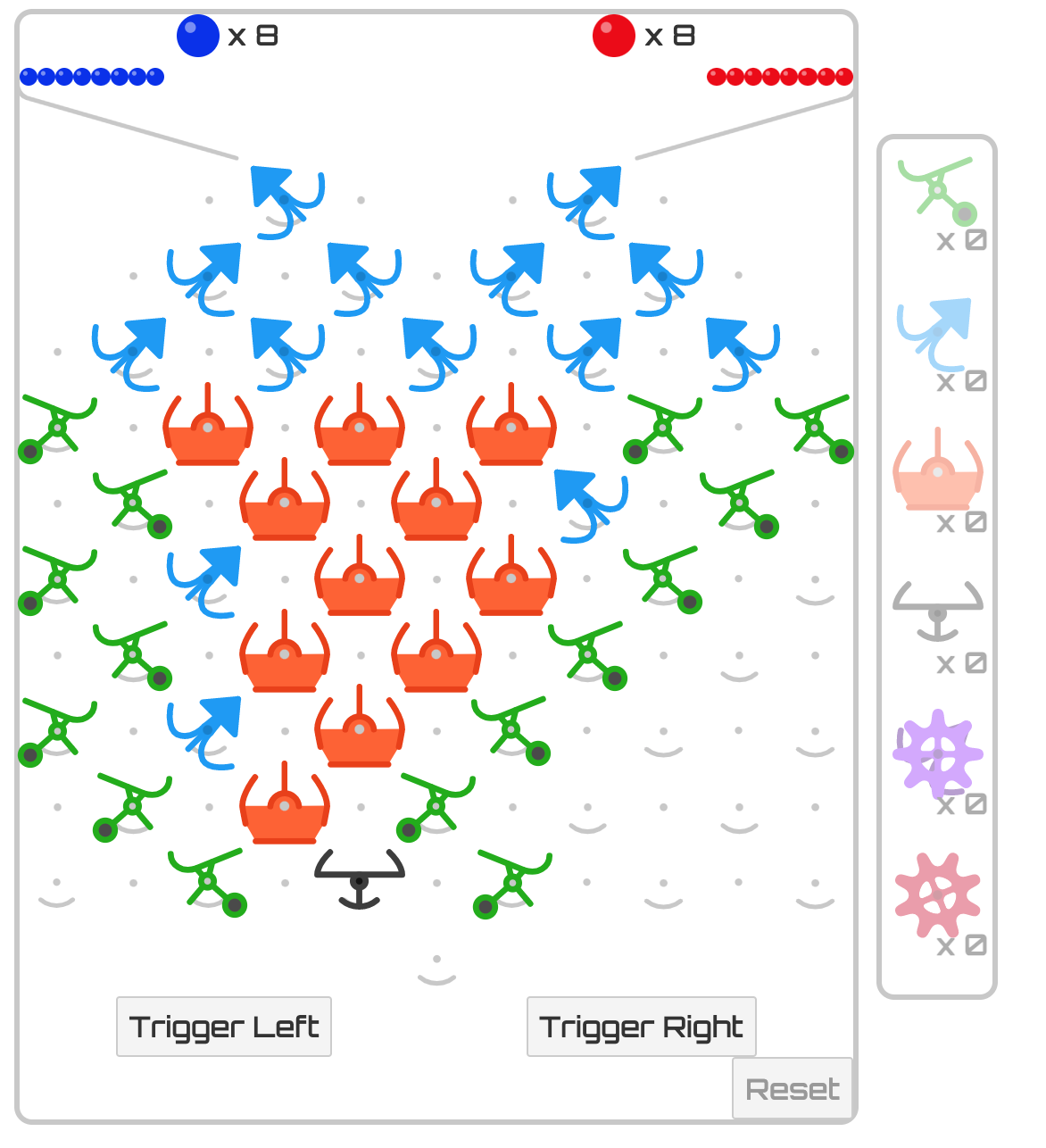
I think this works. It is a bit of a cheat as it starts with only 6 balls in each hopper. I haven’t yet thought of a way to intercept a ball to terminate (if you start with full hoppers). Any ideas anyone?
Hi pt153,
Thank you for your alternative solution. I built it today and it works as I wanted it to.
In my original puzzle I only started with 6 balls each as well. So your solution is an alternative to my original one.
Thank you,
Ollie
Hi @Ollieryan - This version copes with full hoppers and intercepts at end of required sequence. Its not truly elegant though, as the balls drop down the sides. You may be able to jiggle the layout to make it fit properly with more controlled ball drops  ? . The solution is no longer symmetrical, you have to start with a blue ball.
? . The solution is no longer symmetrical, you have to start with a blue ball.
@TTM180 @Alyssa @Ollieryan @pt153
No gears, no dropped balls, stops after the 12th ball, and only uses the parts available in the base kit. However, it is still asymmetrical: only the blue lever can be pulled to start.
The structure in the upper left counts blue balls. The 1st, 3rd, and 6th blue balls trigger a red ball, while the 2nd, 4th, and 5th trigger another blue ball, and the 7th blue ball is intercepted. The structure on the lower right counts red balls. This down-counter is preset to the appropriate values by the 3rd and 6th blue balls. When it underflows, it triggers a blue ball. (Click on the simulator link to see the starting position of the bits)
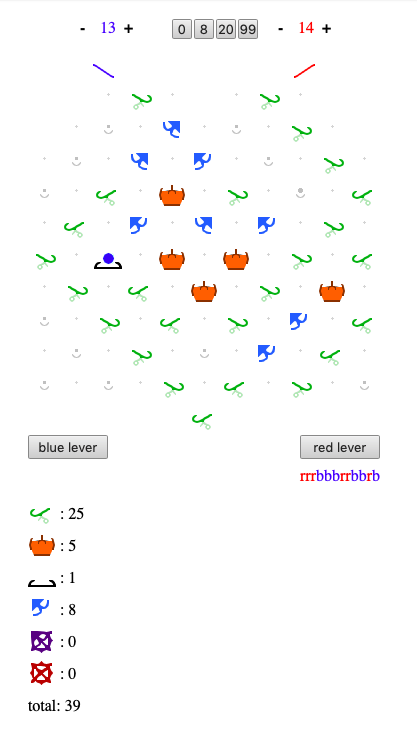
https://lodev.org/jstumble/?board=rre0ere00erelxrell010rrixxrlrlxrxerlr1lere1leerlrel
Hi @RingTheBell - very nice! Thinking back to the shortest impossible pattern debate, you’re solution above (neat, configurable) makes me think its unlikely that the shortest not-possible pattern will be anything like as short as 10 balls.
(Standard board and pieces, full hoppers, terminating, controlled descent of balls etc).