Turing Tumble Community

Proof of Turing Completeness?

#41

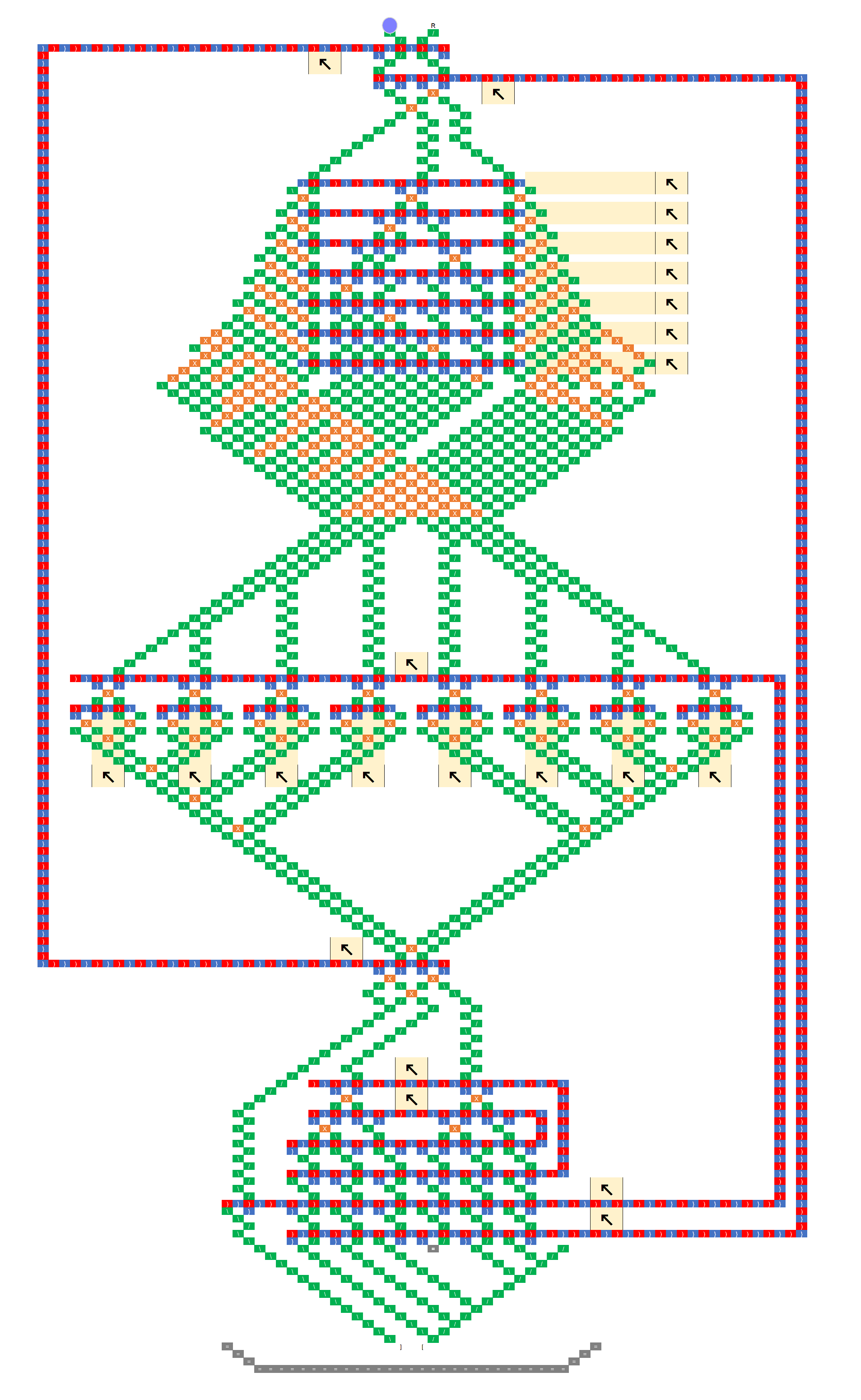
I made a Turing machine table.
[Simulation link]
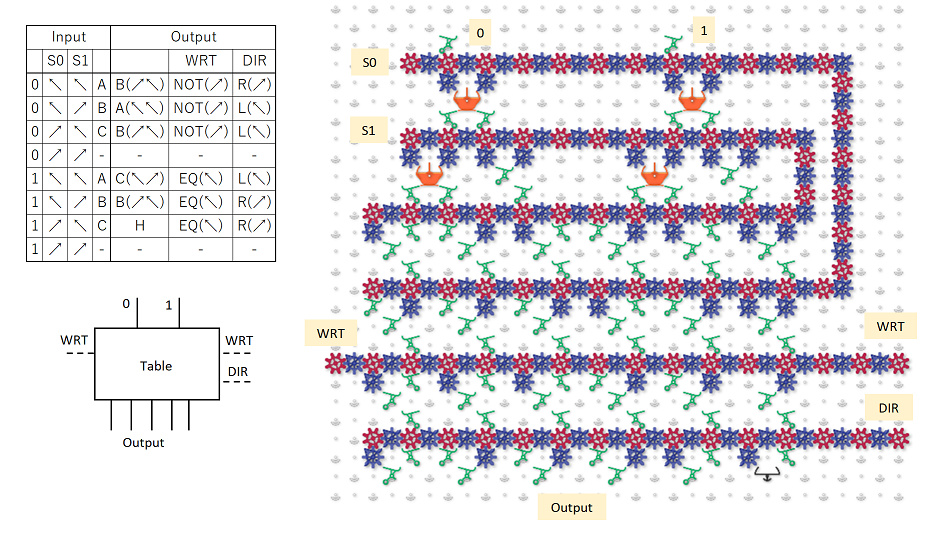
table

The inputs are 0 and 1, whitch value was read from the tape.
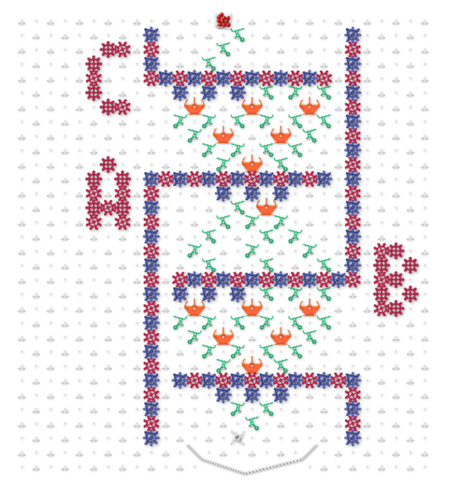
There are 4 sets of gear bit chains inside.

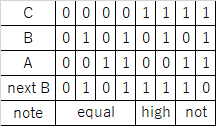
The top S0 and S1 are used to decode the head state of the Turing machine.
I decide like that,
A {S0 = :arrow_upper_left:, S1 = :arrow_upper_left:}
B {S0 = :arrow_upper_left:, S1 = :arrow_upper_right:}
C {S0 = :arrow_upper_right:, S1 = :arrow_upper_left:} .

The other two are connected to an external gear bit chain to rewrite the tape and specify the head movement direction.

Depending on the input and the state of the Turing head, the ball will branch to six ways.
Each sets the gear bits to predetermined.
By this, the ball can set each gear bit chain for any state.

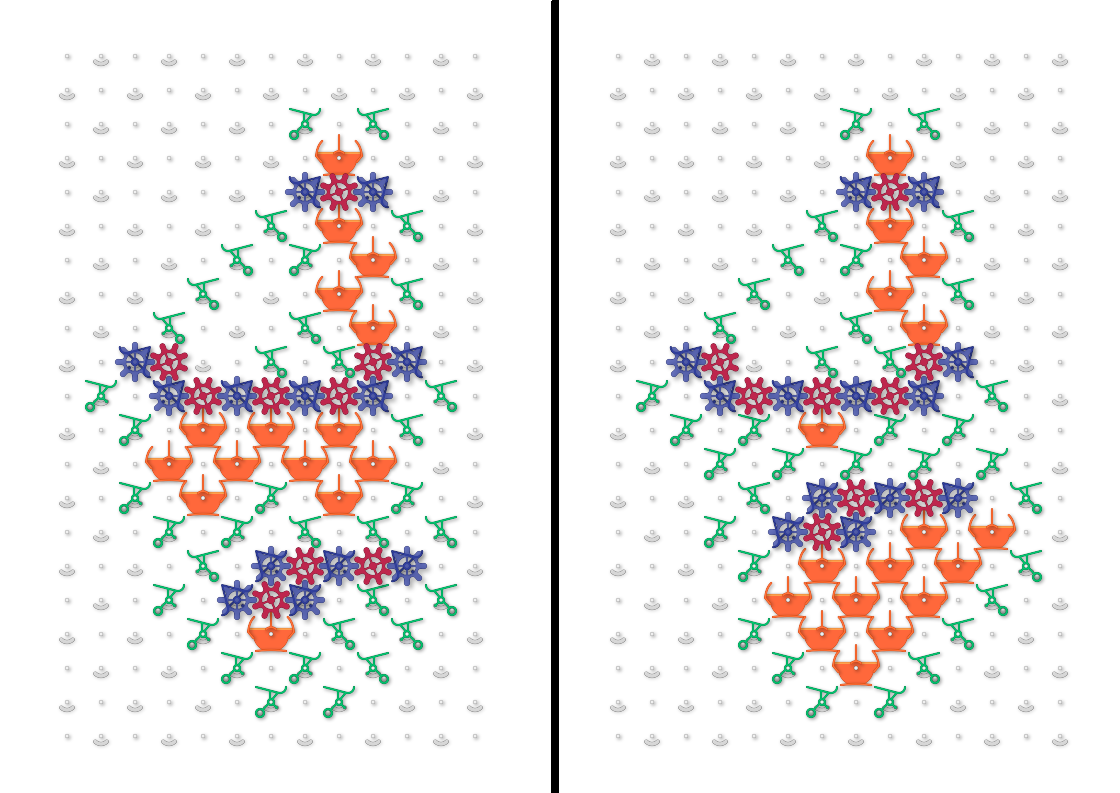
The WRT line is extended to the left for convenience of control.
DIR represents the direction of tape travel. In this time, it is represented by one set because it always moves from side to side.
In general Turing machines, the head may not move, in which case two gear bit chains should be consisted.

The outputs may be indistinguishable, and the balls finally gather in one place.
But there is no space this time, so I did not make it.

=========

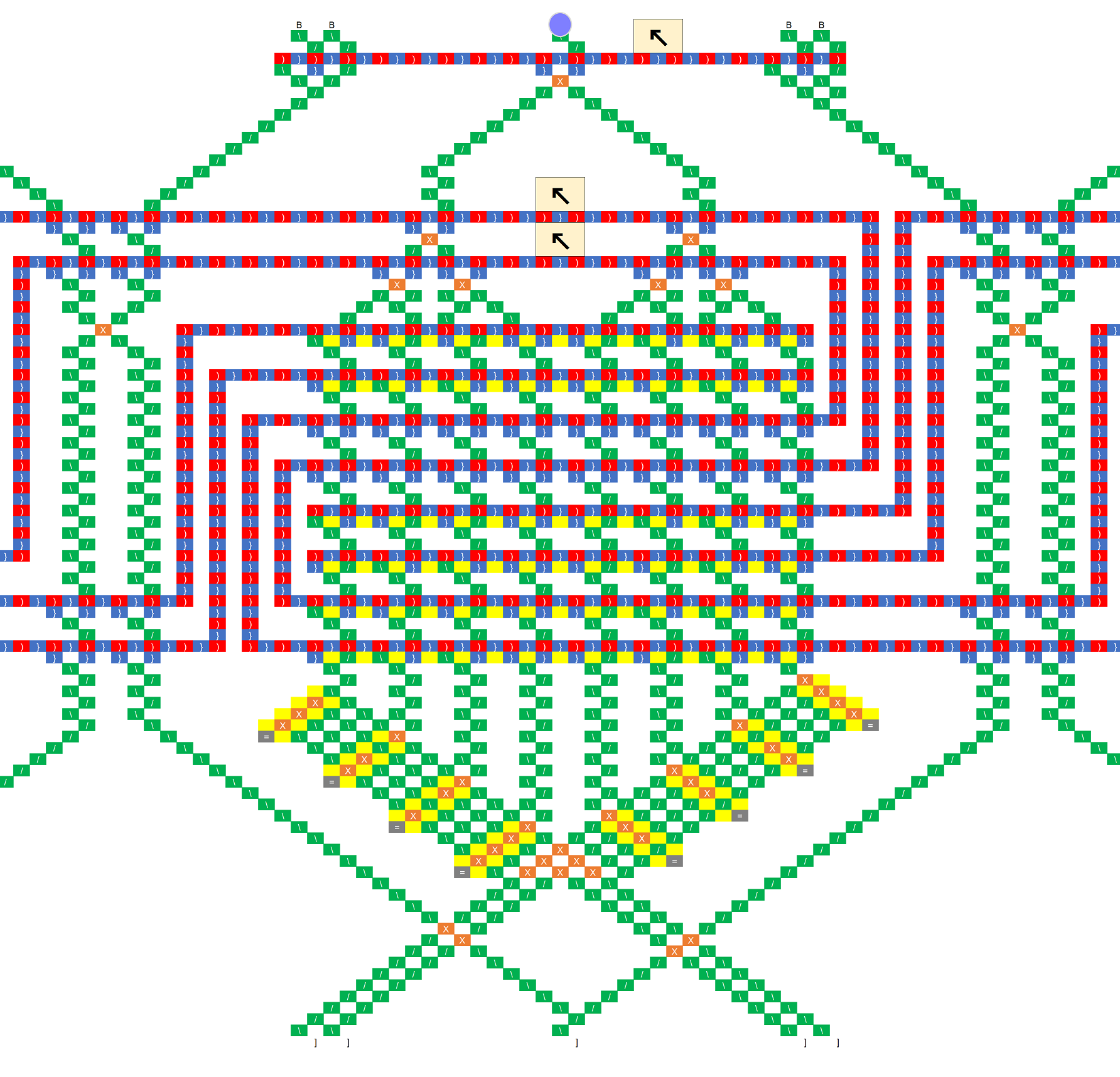
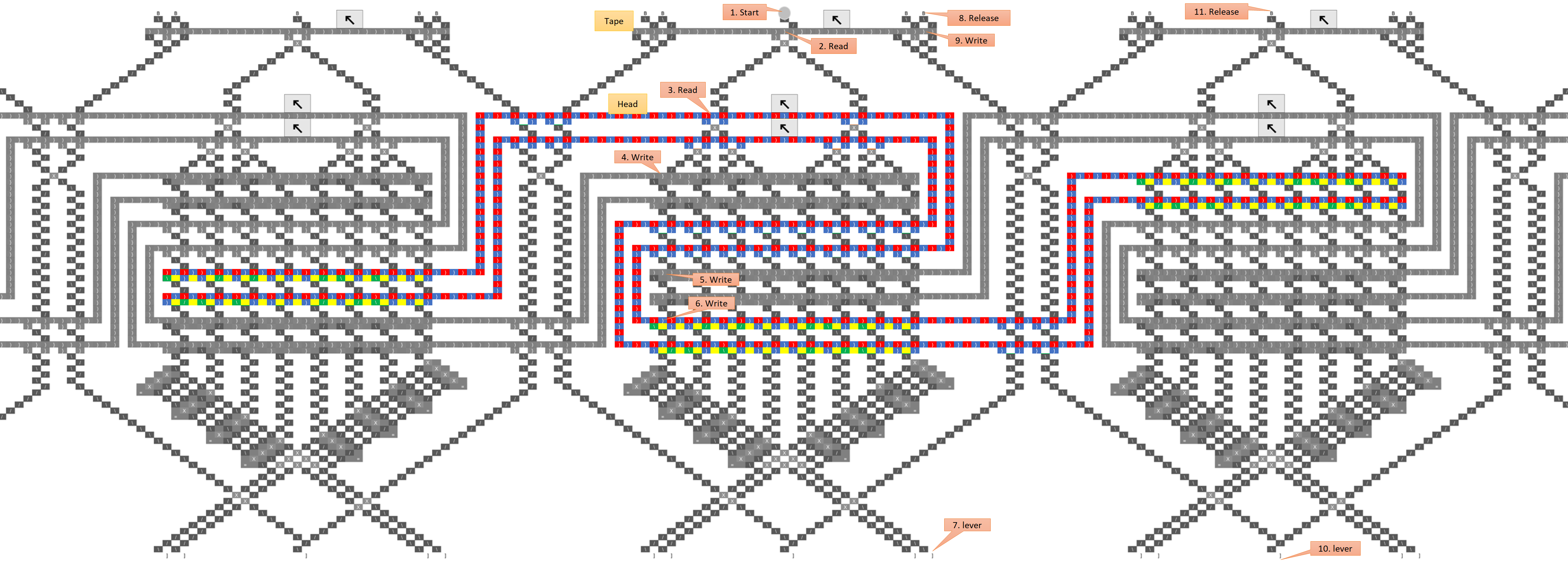
In addition, I summarized the entire configuration.
[Simulation link]
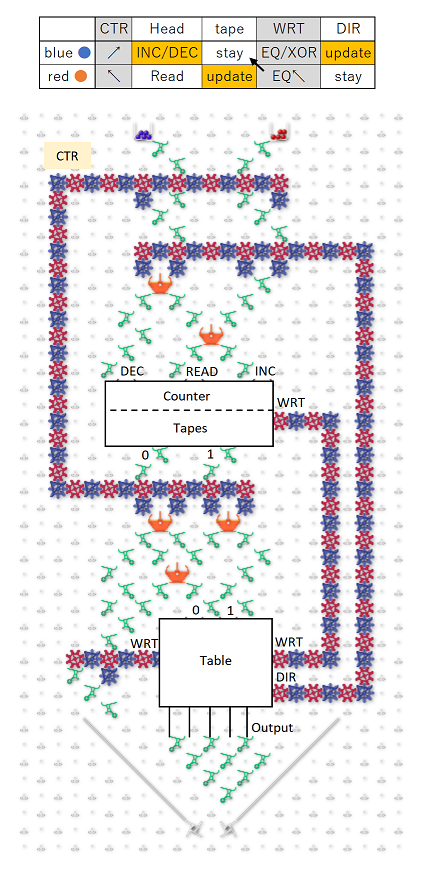
machine

Basically, you can connect the counters, tapes, and tables from above.

However, if I take ball to that basic stracture,
Read tape → refer table → (next ball) → tape moves → rewrite tape → read tape ,
Since tape moves before rewrite, I can not write to the correct location. so then,
Read tape → refer table → (red ball) → rewrite tape
→ (blue ball) → tape moves → tape stay* → read tape ,
We assemble the correct sequence using two balls like this.

CTR wire was introduced for motion control of red ball.
In order to stay tape which shown by*, the red ball makes the WRT line EQ.

If this was actually connected, it should be a one-bit two-value, three-state, four-length Turing machine,
But it is may too large to realize.

#42

I built this Busy Beaver function on simulation.
pict

And I uploaded the video.

I made some mistakes with the above commentary.
In the input to the counter, I should put a blue ball in the middle and a red ball on the left and right.
I also fixed the left conversion part of the counter.

Also, I changed the Busy Beaver function from the above explanation.
The reason I did this is to try the more complicated case, writing “0” other than “1” to the tape.

Thank you.

1 Like
#43

I like your constructions. Of course, the busy-beaver function is not computable, so no TM can compute its value for all inputs.
Perhaps what you have here is a TM simulation for a finite-tape TM that tries to waste time and then halt?

In any case, I think if we’d like a simulation of a general TM, we need to describe the mechanism used to store a potentially unbounded number of bits (that does not depend on the size of the TM). I still don’t see a natural way to do this that is true to the TuringTumble model, and would love to hear ideas.
Lacking that mechanism, while we know that any finite function (or equivalently, TM state transition function, or, computer with finite storage) can be implemented on TuringTumble, the only turing-completeness argument we have is the cellular-automaton one above in this thread.

#44

I think that if the infinite tape is needed, the above configuration needs an infinite height.
It is inconvenient because it does not reach the bottom in finite time.
However, if the tape is finite (as long as it has a sufficient length), the height is also considered finite and not a problem.
I do not know if this is mathematically correct or if it(sufficient length) completely satisfies Turing Complete.

#45

If the tape is finite, then the machine is not as powerful as a general TM; it is only as powerful as a finite state machine. This would not show Turing-completeness. Addressing the unbounded possible computation is exactly what makes this difficult when considering Turing Tumble, IMO.

#46

In constructing Turing Complete, the above board could only handle a finite amount of memory.
Because it starts from one point on the board.
(In the Turing tumble board, the blue ball and the red ball start point are two points, but are substantially the same)
Therefore, consider preparing an infinite number of ball supply units and levers.
00
As shown above, it is feasible.
Based on this, I built an infinite number of the following units.
02
This is an implementation of a Turing machine, and Busy Beaver function is described as a sample.
I explain the behavior in the diagram below.
005

  1. The ball starts when I push the lever
  2. The ball reads 1 bit of the tape and the ball trajectory branches
  3. Read the head status (2bits) and convert it to the ball trajectory
  4. Determine the next head state from the ball trajectory (tape, head state) and write it to the head state gear chain on the left.
  5. Write to the head state gear chain on the right
  6. Write to the current head state gear chain
  7. Determine the tape recording change and direction with the table and press the target lever.
  8. The next ball is released. There can be 4 patterns in recording and direction
  9. Rewrite the tape
  10. Press the lever for the next ball on the right or left
  11. The next cycle begins

I show the capture when I actually did the above.
Since this sample rewrites 6 bits, the tape is 8 bits in the figure.

Before starting
010

After half a step
010h

After one step
011

After 2 steps
012

Completed
done

This is an example, but by reassembling the table
Any Turing machine can be realized.
At this time, in this configuration, the table needs to be copied indefinitely.

To avoid that, add a gear bit to determine the table.
Convert from gear bits to each table like a tournament.
It’s quite large, but it’s not impossible to build a pattern assuming all table conversion patterns.
This gear bit for selecting a table can also be replicated indefinitely with the same “S” chain that copied the head state.

#47

Neat citation!

1 Like
#48

While I found some of the ideas and constructs in the discussion above intriguing, I remain on the side of those who are skeptical about Turing Tumbler being Turing complete - although, of course, open to persuasion by rigorous proof. But I would like to offer the following argument.

First, I think that the references to ‘infinite tape’ are actually unhelpful - to both sides of the argument - (I find this is often the case in discussions of Turing completeness).

It is easy to define a TM that requires an infinite tape - you can do it with a blank tape, and a single transition function that reads a blank, writes a ‘*’, remains in the same state, and moves the tape head to the right. But the point is that this TM, and any TM that requires an infinite tape does not halt. Since Turing’s original aim was to solve what we (now) refer to as the ‘halting problem’, a ‘TM’ that genuinely requires an infinite tape (whether for its input, output, or what we might call ‘working memory’) is of no interest.

Instead of using that term, we should, I suggest, say two more specific and more important things.

The first is that on a TM, the tape is always sufficiently long. If the TM is capable of halting for a given input, which must mean in finite time, then there will be sufficient tape to allow this to happen. In other words, the TM will not encounter an ‘end of tape’ error before it got to the halt state.

The second is arguably more important to this discussion. Any specific TM is defined by:

  • The generic ‘mechanical’ capabilities of any TM (tape, read-write head, movement ability etc).
  • A finite set of symbols (‘alphabet’, if you like), including ‘blank’
  • A finite set of machine states (including a known start state)
  • A finite set of transition functions

This specific TM is then applied to input data, consisting of symbols and/or blanks already on the tape. This input data may be arbitrarily long. And the same TM can be applied to many different starting sets. In particular, if we translate all this into bits, we should say that the number of bits available for the starting tape may, in general, be far greater than the combined bit-count required to represent both the internal machine state and the set of transition rules.

It feels, to me, like the proposed implementations of a TM using Turing Tumble fail this last test. Since (I think it has been agreed above) the balls alone cannot constitute the tape, the tape must be represented by positions of the stateful components on the board. e.g. the ‘bit’ piece. So then:

  • there is no real useful distinction between the TM’s machine state and its tape state
  • the complexity (and size) of the Turing Tumble solution that you need to build grows not just with the complexity of the TM (internal states + transition rules) but with the length of the tape you wish to be able to support - and not even linearly. Adding the ability to have one more symbol to the input data (e.g. if you had a TM to reverse a string) than you had planned should not require building new capabilities of any complexity.

It seems to me that this last point either does, or should disqualify the claim that Turing Tumble is Turing complete.

1 Like
#49

If I understand what you’re saying, then I think you’re confusing the fact that any particular TM computation (that computes a total function) halts, hence uses a finite amount of tape, with the (incorrect) notion that for any TM, there is a fixed bounded amount of tape that it might ever use regardless of the input. Any interesting (function-computing) TM must be able to accept inputs of arbitrary size, hence a fixed tape size would not be sufficient.
If in your model, you assume each TM comes together with a fixed, finite amount of tape, and is required to do all of its computation within that space, then the TM isn’t any more powerful than a finite state machine.

The question of whether a particular device or process is Turing-Complete usually does involve some type of assumption that deals with the issue of potentially unbounded (but finite in each case) computation. For example, in showing that Rule 110 in cellular automata, or Conway’s Game of Life, is Turing-Complete, one needs to assume that the grid available is infinite. I believe that for Rule 110, one further assumes that the grid is initially pre-set with an infinite repeating pattern that represents a blank tape. Is this kosher? The theoretical CS community seems to have agreed that it is.

I think the simulation presented by @jcross, which involves using an infinite repeating pattern of parts on a board of fixed width but infinite length, is a reasonable model and probably shows Turing-Completeness. I say “probably” only because it hasn’t been written up, submitted, and peer-reviewed, and consequently carefully checked for correctness.

IMO, all other contributions to this discussion do not adequately deal with this issue - and ultimately involve constructing only a computer with finite capacity - hence no more powerful than a finite-state machine.

So, I think the claims that Turing Tumble is Turing-Complete are premature given this state of affairs.

The discussions we’ve had here attempt to determine other “reasonable” ways to deal with the unbounded tape question. The finite state control only needs a fixed number of TT parts, but the model needs to allow for arbitrarily long inputs. Hence thoughts of a potentially shiftable horizontal array of bits below a ball drop to represent the tape. (But this model would then need a new lever or part that does a tape shift one way or another.) Or, an infinitely long repeating pattern of some sort representing the initial input and infinitely many blank cells (as in the @jcross construction). I think that all of these are reasonable approaches to resolving the question.

#50

Just to be clear, I absolutely wasn’t saying that (or wasn’t meaning that if that’s how you read it). My assumption of a TM is that the input data maybe arbitrarily long, though finite, but that it is not possible to pre-define a total length of tape (for output and/or working ‘memory’) within which the machine could halt. (I was merely trying to get away from the idea that it needs to be ‘infinite’ which seems to confuse some people. Perhaps ‘indefinite’ would be a better word.)

My more important point is that there is a qualitative difference between the tape and machine state. IMO, if I set you a realistic problem e.g. to define a TM that would reverse a string - you should not have to ask me ‘how long a string’ in order for you to order sufficient parts from TT to build it. If TT is Turing Complete - again, IMO - you should be able to design a TT board that would work for any finite string.

You, I think, pointed out early in the discussion that the problem was defining the input/output of the machine, and I think that really put the finger on it. There is nothing corresponding to the tape. To me, it is not satisfactory to define the tape as being of the same kind of thing as the machine state.

By way of a thought experiment. Suppose that the blue and red balls had different weight, and that there was a simple TT component that could drop the ball one side or another depending on its weight. And supposing that you had three feeds at the top - one for the input data (a sequence or red blue) and two, indefinite, reservoirs of red and blue balls, and if, also , there was a way to feed balls back from the bottom to the top (tape) …

Then, I believe there is a good chance that the whole thing could be deemed to be Turing Complete (though I am not asserting that this is definitely so).

#51

OK - now I understand what you were saying - and agree. Sorry for my misreading. Also, agree with the ball thought experiment.

But, do note my later point that for the cellular automata model, people have incorporated an infinite array of a repeating pattern as a place-holder for the infinite tape in a proof of Turing-Completeness. In a similar vein, I think that if one could come up with an infinite repeating pattern of TT parts (say, that grew horizontally as the depth grew… to allow for wider and wider computation) that could simulate a computation, it could be the basis for a proof of Turing-Completeness despite the fact that it is using an infinite number of parts. Or, similarly, the @jcross construction, which may already do that.

#52

Thanks. To your point, I would agree that if the implementation of the ‘tape’ was made of TT parts, and satisfied these conditions:

  • was clearly distinct from the parts of the machine implementing machine state and state-transition rules
  • could be extended, without any change to the former, both in order to specify the input data, and the ‘tape’ needed for working memory and output data
  • for any fixed ‘alphabet’ of permissible symbols, extension of the ‘tape’ (in terms of the number of additional TT parts required) was linear w.r.t. the number of tape cells added.

…then my concern would be met. Does your reading of the @jcross design indicate that it would meet all three of those conditions? If so, I must re-read it more carefully.

#53

Yes - those specs are consistent with what I had in mind.

The @jcross design is a different kind of thing - because it is not directly simulating a TM, so I don’t think your bullet points apply. Rather, it is simulating a 1-dimensional cellular automaton programmed with rule 110. Each “cell” of the automaton is represented in the design by a whole mess of parts - roughly 45 wide and 25 high. An infinite stack of those corresponds to the infinite linear array of cells. The cells are set according to the initial input to the cellular automaton. A ball falling to infinity corresponds to an update of the pattern according to rule 110. As Jesse points out, we don’t need to wait for the ball to “finish” before triggering a new ball - probably could just insert a single trigger about, say, 100 layers down which would release a new ball to update the cellular pattern to the next generation even while the previous ball is continuing to update cells further down.

The implementation is a fixed one - a single pattern of TT parts, with repeating blocks. The way it is “programmed” is to flip bits in the cells to correspond to the cellular automaton’s input string.

It’s been quite a while since I looked at it and thought about it, but it did seem to me to work, though I didn’t check it with a fine-tooth comb the way I might if I was reviewing a paper. Nor is a proof presented of its correctness - which probably would be tedious to generate. It would most likely follow an inductive argument that after n balls have passed a cell, the bit represented by the cell is the same bit that would be in the n_th generation of the initial pattern under rule 110.

To have any confidence in this, I think more people should look at it, and perhaps it might be worth trying to flesh out a correctness argument.

It is also worthwhile pointing out that the proof of Turing-Completeness of Rule 110 assumes that the initial pattern of the cellular automaton is infinite though made up of repeating blocks of a finite pattern. So, the simulation of this by TT would require setting of the infinite parts to be a repeating finite pattern that depends on the initial input string. (And, yes, it is a linear relationship.)

Edit: earlier I was concerned about whether we needed TT to simulate a two-way infinite cellular automaton. But the proof of Turing-Completeness of Rule 110 simulates a cyclic tag system, which appears to only need an unbounded potential on the right, not left, so the proof probably uses a one-way infinite cellular automaton. This eliminates my earlier concern about the @jcross construction.

#54

I convinced that the previous theory constitutes rule 110.
However, as it is, it’s too large to be implemented and verified.
Therefore, I decided to make the circuit smaller.

Assume a device that bits are “C”, “B”, and “A” from the top.
The sequence would be write(and read) “C”, read “A”, write “B”.
Then, according to rule 110 in the table below, when “C” and “A” are read, the “changes” in “B” can be summarized into only three: set, reverse, and invariant.
image
In other words, we only need three routes after “C” and “A”.
Based on this, I constructed the simulator as follows.
More smaller in the horizontal direction, more it can be shrunk in the vertical direction.
image
https://jessecrossen.github.io/ttsim/#s=29,32&z=24&cc=18&cr=16.5&t=1&pt=9&sp=1&sc=0&b=data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAB0AAAAhCAYAAAAlK6DZAAABEUlEQVRIic2WbQ7DIAiGOUqPsN3IHzsIF9vZ2I9NU6kIAjZrYhpS8eFN+RDI/cBeTxR2wXvuLvpZoATXbRpQ8jNDecQm4MBvCUoA3wMW3tXPD2WR83dVDr/jqh1TOiJb7AylTQlTdLGzlVaApLBLsgylHCwpZHHkQM/AocK2KVqnq2VDGzqSVD6anxmq9l5hw7bey5NK8zNDtd7LA5D8lqDniPnBU/sOpdzOUeqdNh6oVB7alBE1WKBdxCtTJgJtihanTAg6zF7LlIlAL9lrnDIh6LAjWaZMBNplq2PauKD/NWWUukxX2j7N/uUOpZp32h0JEaffSynqGa6LGSK2VUrpluUBAKLX8aDj+SAAuGV9AEvlRjQgvigPAAAAAElFTkSuQmCC

1 Like
#55

here is video.

1 Like
#56

@Yama-chan Thanks for making this video. We get people asking about the Turing Completeness all the time on social media. This will be a good resource to share.

#58

I have made another Turing Tumble configuration that emulates rule 110. There are two configurations. The one on the left can be chained together for however many cells as you want. The right configuration can be placed on the bottom, and allows the CA to cycle, so that the bottom cell is connected to the top and the top to the bottom, in a sense. I will post a video of it running in just a moment.

rule110TuringTumble

Here are links where you can play around with each configuration:

https://jessecrossen.github.io/ttsim/#s=21,26&z=32&cc=12&cr=13.5&t=3&sp=1&sc=0&b=data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAABUAAAAaCAYAAABYQRdDAAAAmUlEQVRIie2UUQrAIAxDc1SP4sV6tu5nFRfdaqdjDOZPEewjTajQBw5+6LtQ7M8h121xpdlvCUETRAXQBFkDLSNn34IhqAHMU88CF9oomlXKjWxBGGqhMBACN6wu1Lyr0+bam8RV2oSSV6V/ArztKSs9vUeVll2nnecagtaNGaoKHOuMUgbNK2UvHeAQtAYv/08ZvAQaOd+BbviY8m6C+clhAAAAAElFTkSuQmCC

https://jessecrossen.github.io/ttsim/#s=21,26&z=32&cc=10&cr=12.5&t=3&sp=1&sc=0&b=data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAABUAAAAaCAYAAABYQRdDAAAAoUlEQVRIie2USw6AIAxE56gchYv1bONGMFQ+LWCMid1UTX2ZtgPgA4Ef+g4UZxnEpsGuNNpLTZUBQgEYIHugueVoH0G3IgHSTK0jaFbdFK0q1T/qEbihaSkaCIF5WShfUIBrudbJUGk2ulrO7bsHWgO0sgtKXi1GkATKzP4Iuko1KD8MXNBWqg2vsltpjgnglNL1s69ttes+9fjTDJ2J70APSSPyeNEeI+sAAAAASUVORK5CYII=

1 Like
#59

Here is a video of it running: Turing Tumble emulating a Rule 110 cellular automaton - YouTube (do remember that in YouTube you can adjust the speed of playback with the gear icon.)

There are six sets of groups of 5 gears, each group of 5 gears is the value of the cell. If the gears are pointing left, it’s a 0, if they are pointing right it’s a 1. Cells from top to bottom correspond to rows in the CA going left to right.

This image helps to figure out what’s going on.

rule 110 bounded shifted

The left image shows rule 110 with a cyclic boundary that only has 6 cells (left connects to right, right to left.) The right image shows the same thing, except the cells are rotated right by one step each time you go down a row, so row 1 is shifted 1 to the right, row 2 is shifted 2 to the right, etc. The shifted version corresponds to the Turing Tumble configuration.

It takes two passes of the balls for each update step.

Here is a link to the whole setup so you can run it yourself in your browser:
https://jessecrossen.github.io/ttsim/#s=32,115&z=6&cc=31&cr=60.5&t=3&sp=1&sc=0&b=data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAACAAAAB0CAYAAADkZTAVAAABXklEQVRoge3bzW0DIRCG4SmFEqI4ObgbDi6ExqjtyyVYmCxKdpYfRXpXstAeYD4z2H72YNPmy/5tgJSSJCnGeHg/PcDR9JzPL3e5Bfa9hDmKDwkgSUr+ZS4HiJaVzRQtrw/w3Pbkb4M7QClWzoC3Da5ZP97pyh1oi7RtmBqgHLi2uGVzH8Q/Byi9rk99O9ahhgeoQzy3O+34FHSKLzkD7Q5072cFqIu0vwHtOC1AXSSZJLPX8exa5yccFNfqHWh77yzuDlCH2OqBNsTyAC8hEBEiQkSICBEhIkSEiBARIkJEiAgRISJEhIgQESJCRIgIESEiRISIEBEiQkSICBEhIkSEiBARIkJEiAgRISJEhIhWiqjngD0e6IzTAki/e+BMG4Z5wGvDIR64omP/V/EgmrsClL917Xku6ITY4oESYquIygp5hwdGXPsDmEmP8K6Pz6DbPegR3hRud5nZktcXS/QSsi3hrUAAAAAASUVORK5CYII=

Just click on the red balls to get it started.

1 Like
#60

The links to @OUDON 's thesis are now broken; is the PDF available anywhere? This is all a fascinating discussion.

#61

This is a very interesting arrangement.
I have not fully grasped the logic behind this, but from what I have seen so far, it perfectly replicates Rule 110.

The point of this construction is that when the next a’n is generated from each bit where the nth is represented by a_n, it is usually
a’n = Rule110(a(n-1), a_n, a(n+1)) ,
but it is
a’n = Rule110(a(n-2), a_(n-1), a_n) .

This causes each bit to move to the right every cycle.
This does not make sense mathematically, but it is important because it eliminates the need for information about the gear bits located below in the Turing tumble.

Rule 110, which I constructed in #54 above, is in the form of an interlocking “C”, and I tried to reduce the number of gears.
However, it requires about 50 gears per gear bit chain.
To be honest, this would be impossible to actually make work with mechanical energy, no matter how much friction and rattling we reduce, or how heavy the balls are, or how much we improve the energy efficiency of the gear bits.
On the other hand, xylochoron’s method may work well enough for a chain of up to 11 gear bits.