I can’t say I follow all the theory here about Turing Completeness, but I believe I have designed a “metapixel” that can implement any 1D elementary cellular automaton. This includes Rule 110, obviously, so if it works I guess it would constitute a practical proof? Well in any case it’s the best I can do because a formal proof is out of my league at this point.
I’m not sure how well it handles the infinite extent requirements, but it lays the cells out vertically, so the width is smallish and fixed. The height varies with the number of cells being simulated, and can in theory be extended indefinitely. It requires only one ball per generation, and side/color is irrelevant. There will be some issues with edge conditions at the top and bottom, which could be crudely solved by padding. There also may be a proper solution to make it behave like a ring, but I haven’t fully considered that yet. It could involve either some fanciness with ball side/color or some VERY long strings of gear-bits.
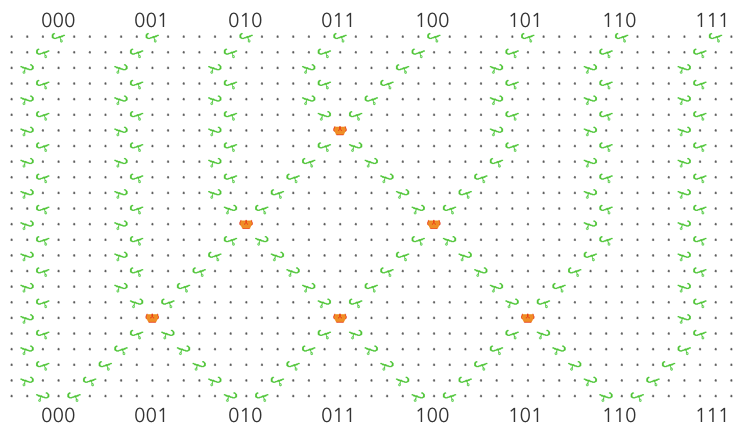
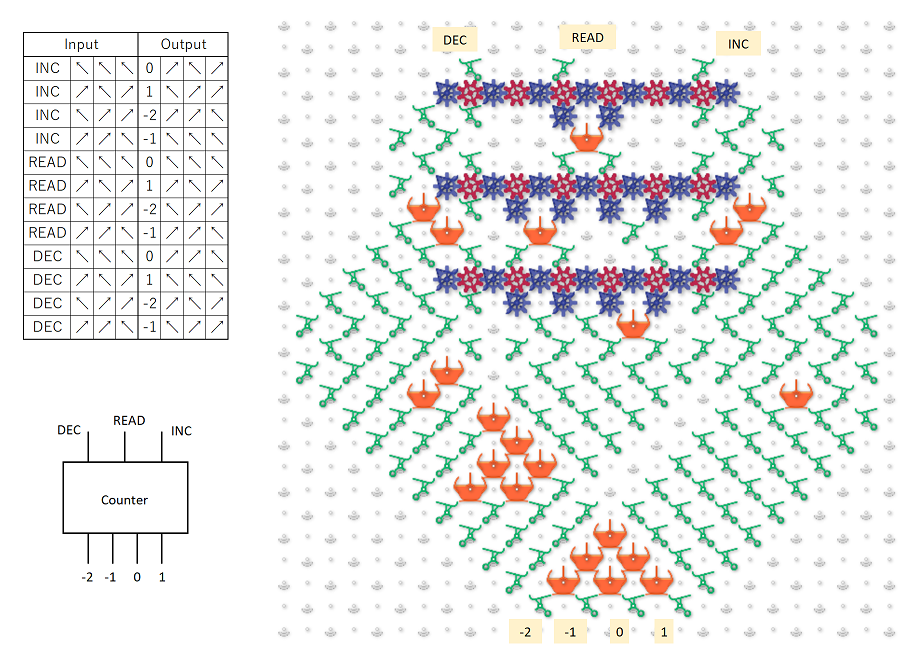
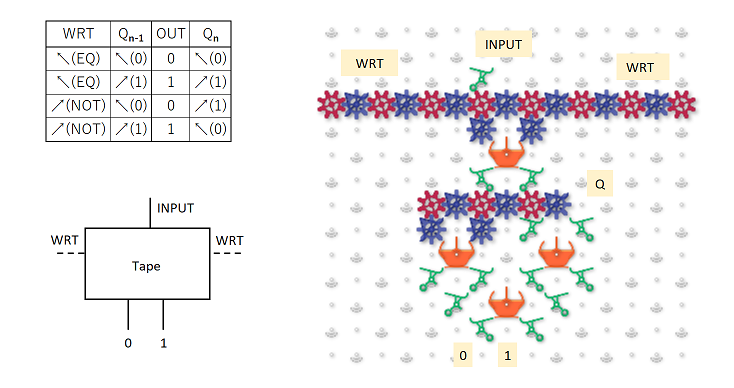
Okay, on to the solution. The mechanism effectively stores a 3-bit register, using horizontal ball position to encode its contents. The core operation that can be performed with this register is to shift one bit onto the end of it, moving the rest one position left, such that ABC become BCD. This shift operation is accomplished by the following unit (there are a lot of parts so I’m using a schematic representation of the board):
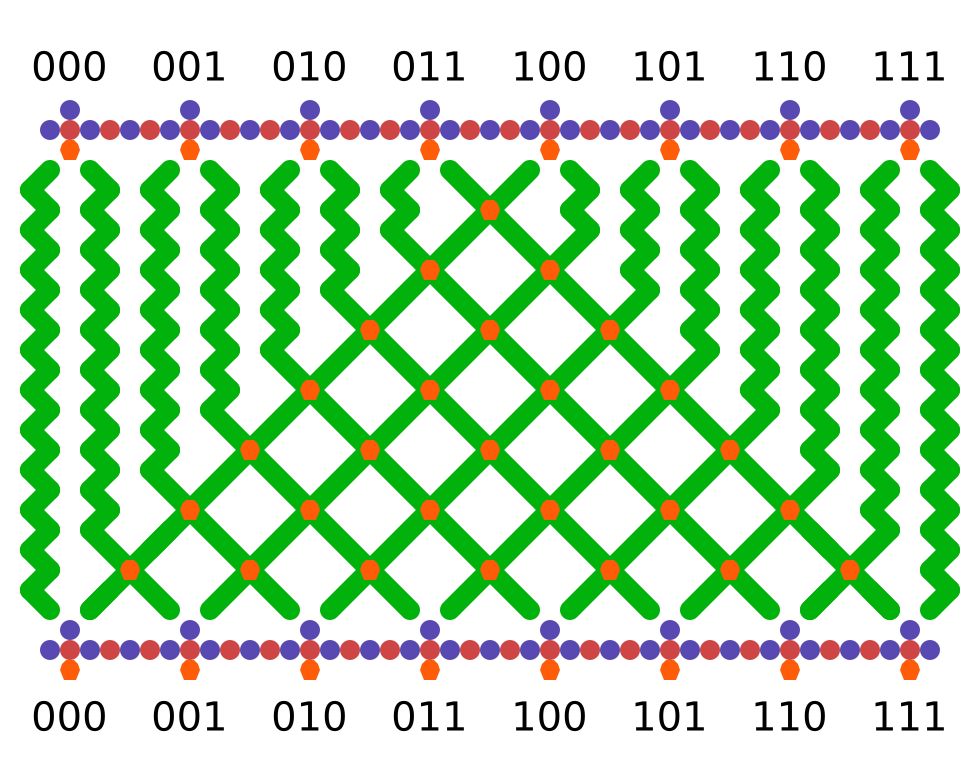
So regardless of which position the ball arrives in, the value from the set of gear-bits at the top is non-destructively read and the ball is routed such that its value is shifted onto the end of the register. In this way, the running value of three cells can be stored. To implement the CA rule, we route the ball through units that perform a destructive read:
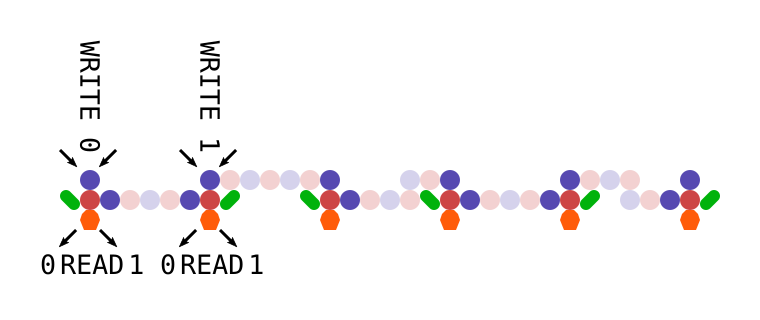
There are two types of units, one which writes a 0 and one which writes a 1, but either will use the prior value of the bits to route the ball in the same way as the units above. As you can see, they can be arranged on the same spacing, and any combination of units can be geared together without interfering with their function. By placing eight writers into the appropriate positions, we can implement any elementary CA rule.
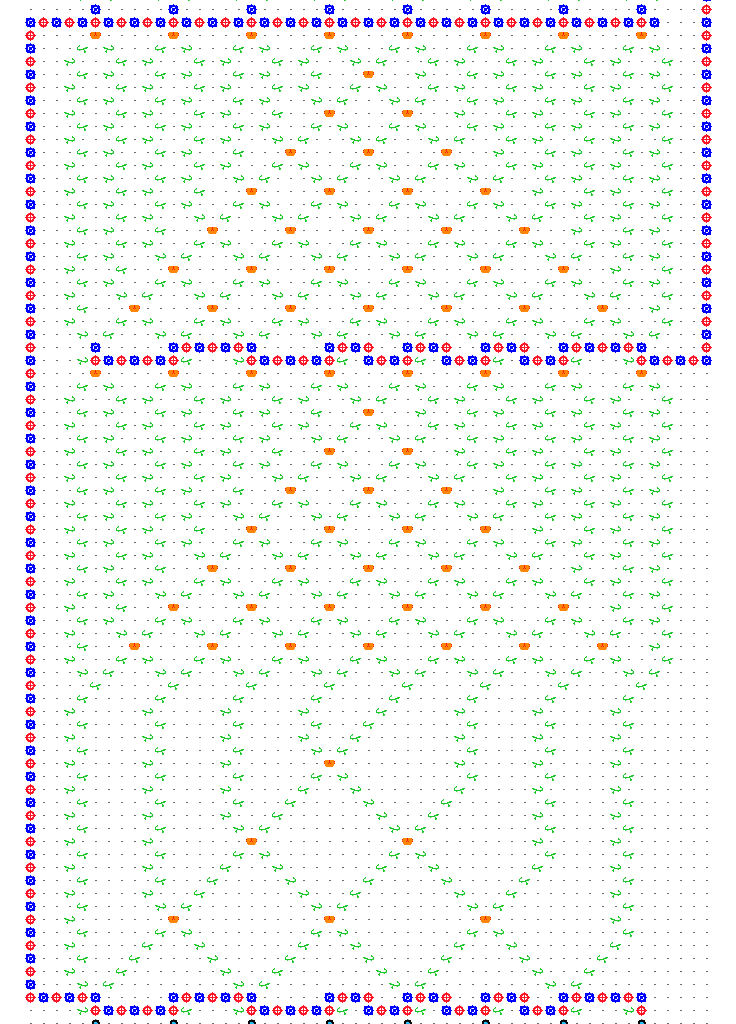
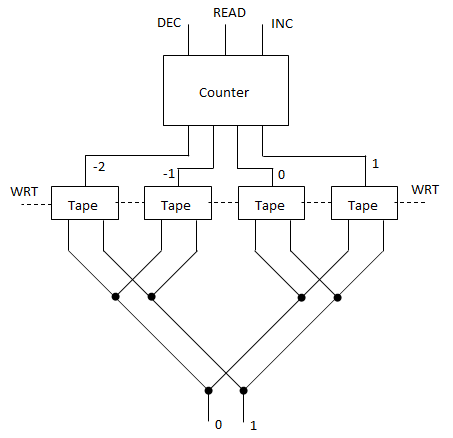
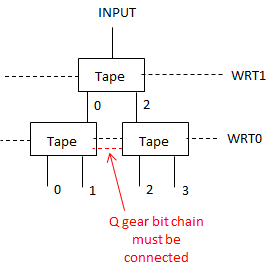
The remaining step is to arrange these units in a continuous chain and propagate some information upward as the ball drops (and we can’t cross gear chains (yet)). This is done using a topology of interlocking C shapes. Each C is a long chain of gear-bits representing one cell in the automaton, with a read stripe at the top and a write stripe at the bottom. Half the cells push up information on the left and half on the right:
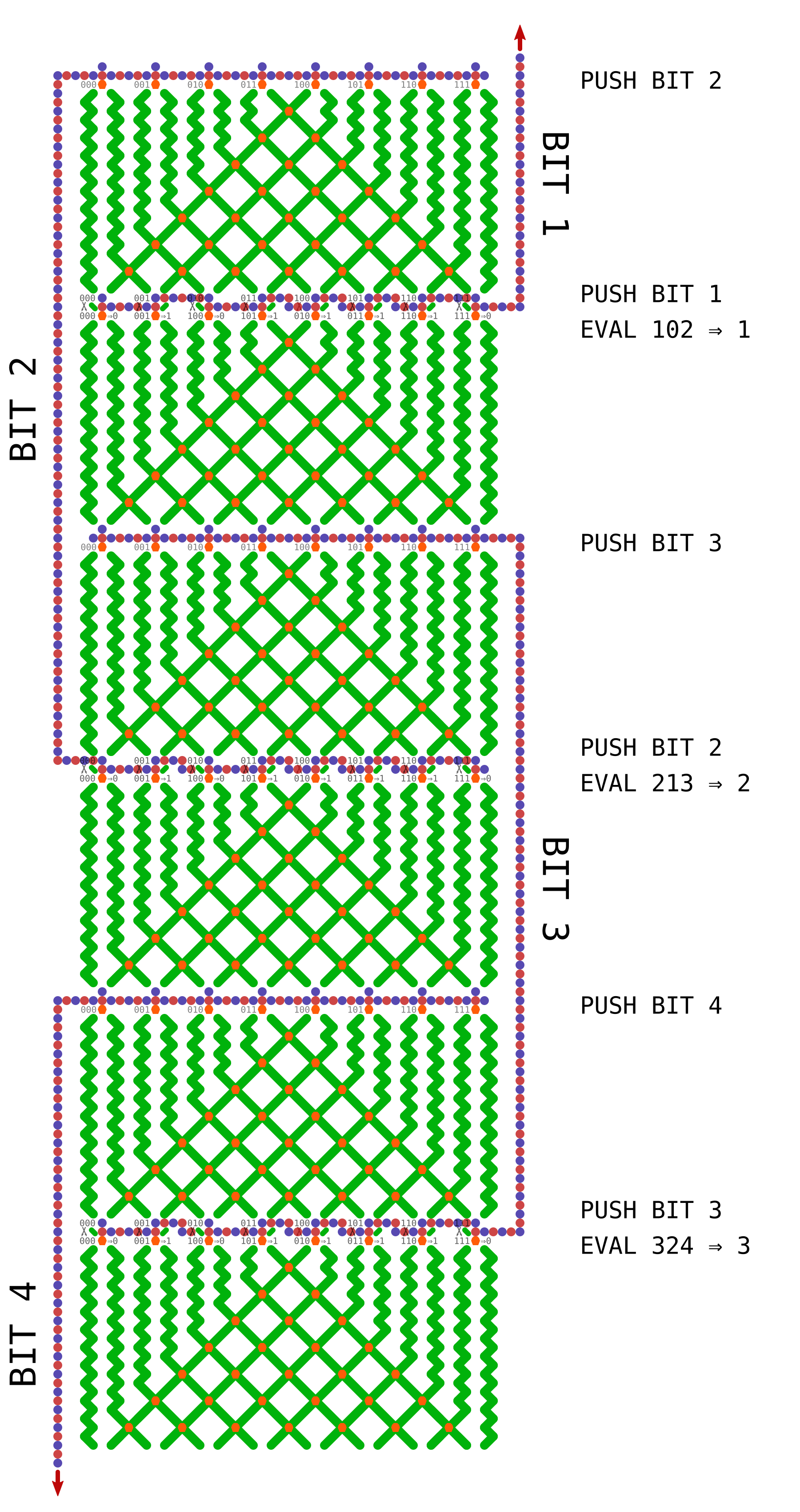
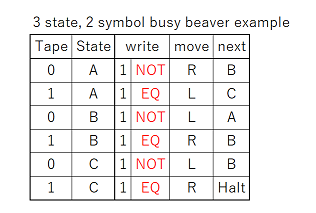
That’s a big image, but metapixels do seem to spread out… I just realized I probably could remove some space between parts and make this about half the size, but I drafted it with extra room just in case. Anyhow, because of the order in which the bits are pushed onto the stack, the rule isn’t laid out in the usual way. Each time it’s evaluated, the order of the cells is BAC => B, CBD => C, DCE => D, etc, so the current cell and its “left-hand” neighbor are always switched. It’s pretty trivial to map the rule, and I figured it was easier to do that than something like using multiple types of routing panels to get the order into the canonical form each time.
So, I’m fairly sure this would work but would appreciate more eyes on it. Also, is there a simulator that can handle arbitrarily large boards? That might come in handy if we’re going to continue speculating about theoretical problems.
EDIT
I think making it into a ring works out okay, although it involves very long chains. But hey, if we’re imagining infinite boards we can imagine constant friction too. Here’s one topology that I think would work, forming a ring of eight cells.
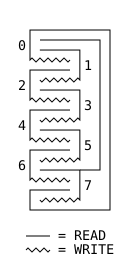
This game is keeping me up at night Paul! It said “addictive” right there on the box, but did I listen?