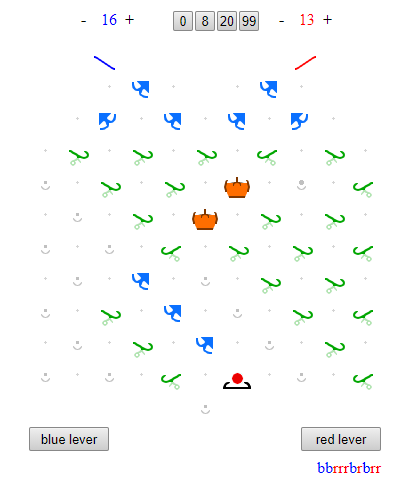
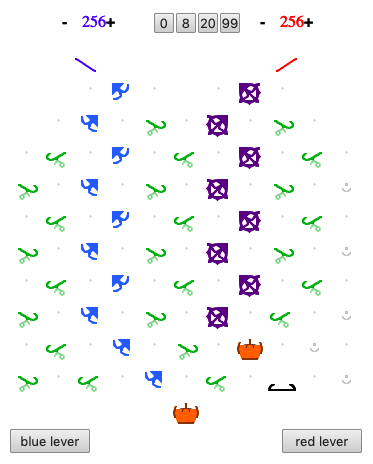
The tl;dr version of this comment is that since there are only 18 bit pieces supplied in the game, only patterns of length at most 2^18 may be generated.
The comment by @Florentin seems to be the crux of the problem of thinking about this - what tools do we have? The only tool I can think of offhand would be in essence a counting argument, similar to the pumping lemma for finite state machines. But first let’s firm up the statement of the problem:
Say that a finite pattern p can be generated by TT out of the box if when pressing either the left or right lever to start, with all balls initially at the top, the machine halts by routing a ball to an interceptor, and the pattern p is what has been output. So, the longest pattern that can be generated would have length 39, since 40 balls come with the machine. But let us consider a more interesting extended version of the problem which allows longer patterns to be generated if the machine started with more than the supplied 20 blue and 20 red balls, but halted with a ball in an interceptor.
Now, following along a simple counting argument, there are only 18 bit pieces (10 regular, and 8 gear) supplied in the box. So, regardless of how the pieces are laid down, if a pattern p of length more than 2^18 is being output, then the pattern of bit settings must repeat some configuration, so the machine is in a loop, and will never halt. We conclude that regardless of the number of starting balls, only patterns of length at most 2^18 can be output (with the machine stopping via interceptor) according to our definition.
While that number is way high, it is a very weak starting point towards arguing about patterns that may not be generated.
Finally, this suggests another challenge - sorry if it has appeared already. What is the largest number n such that the machine when run, outputs n balls and then stops via interceptor. We can consider two versions of this, both on the standard board size: Version 1, you are supplied only the parts in the box. Version 2, you may use any pieces you’d like, as long as you use the standard board. I can see how to make a 10-bit counter that halts on overflow. Is a number higher than 1024 possible?