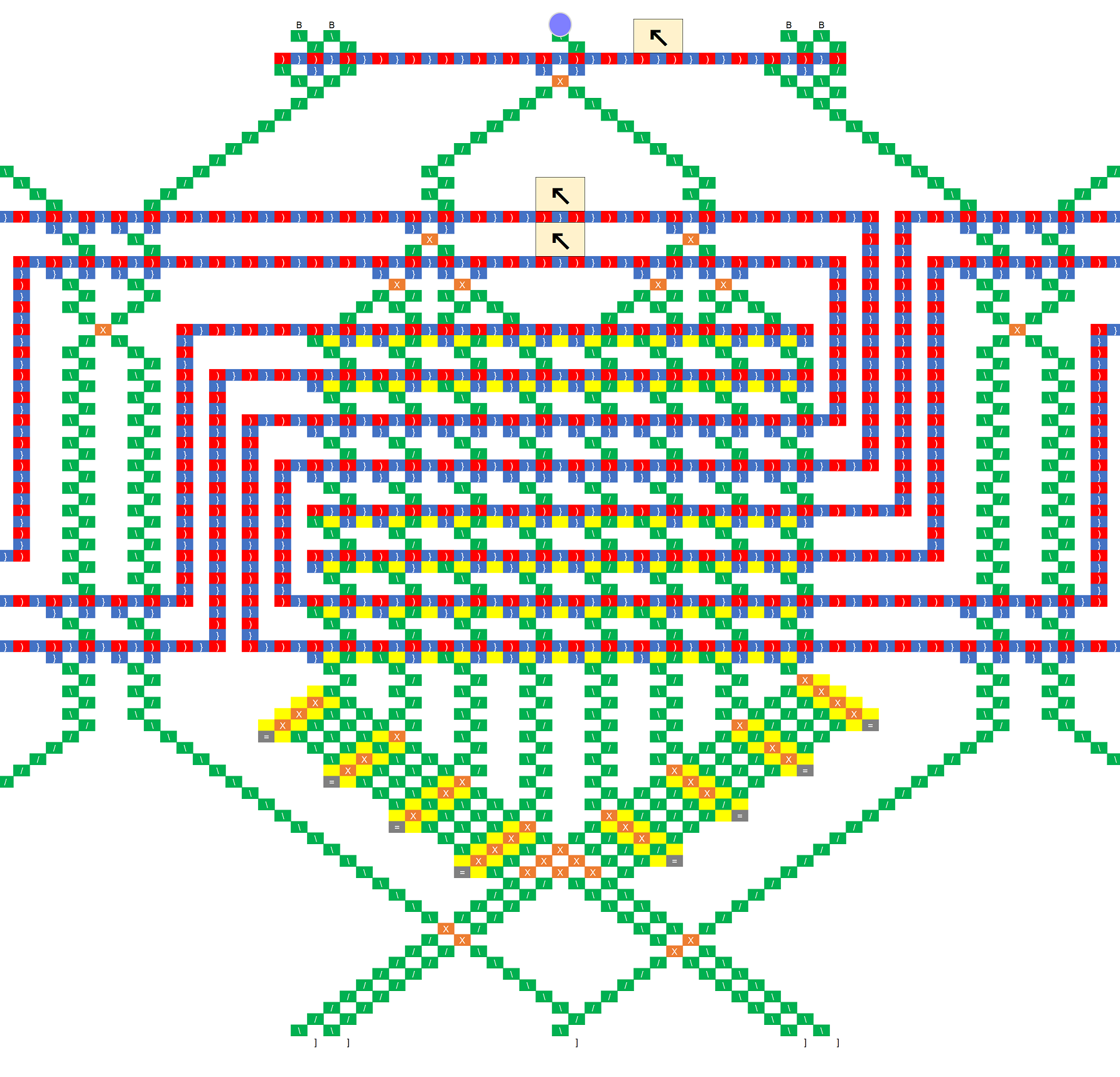
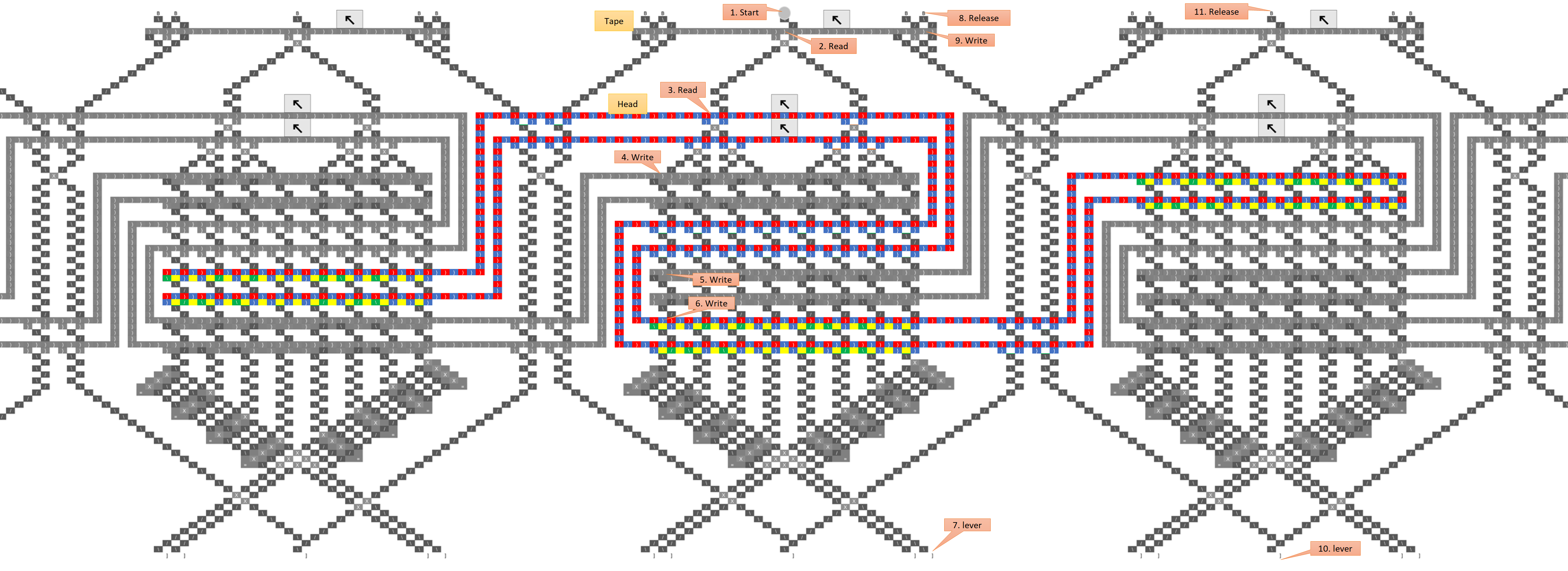
Regardless of whether this is right or wrong, or works or not, this seems ingenious. There is a lot here to digest, and I’m trying to understand it, and my head hurts  I’m a bit confused and fuzzy about the high-level idea though. Here are some basic questions which may help me: Let’s suppose that you are only simulating the evolution of a fixed-length string (I guess we assume for the purposes of rule 110 that non-existent neighbors at the ends are treated as 0s).
I’m a bit confused and fuzzy about the high-level idea though. Here are some basic questions which may help me: Let’s suppose that you are only simulating the evolution of a fixed-length string (I guess we assume for the purposes of rule 110 that non-existent neighbors at the ends are treated as 0s).
-
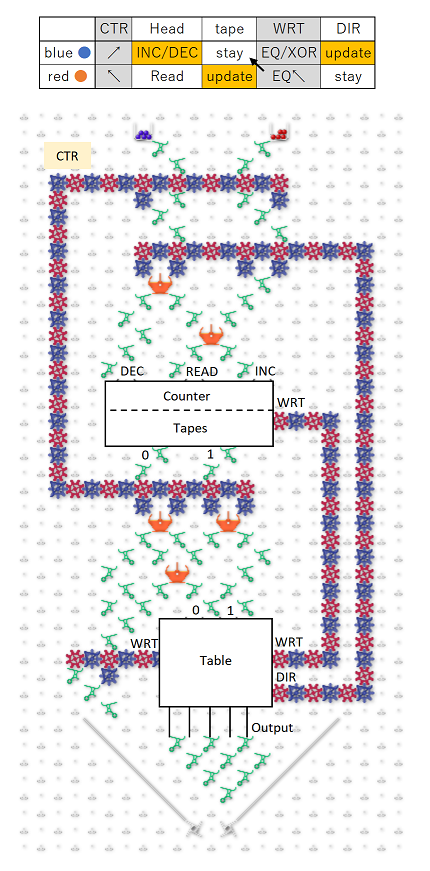
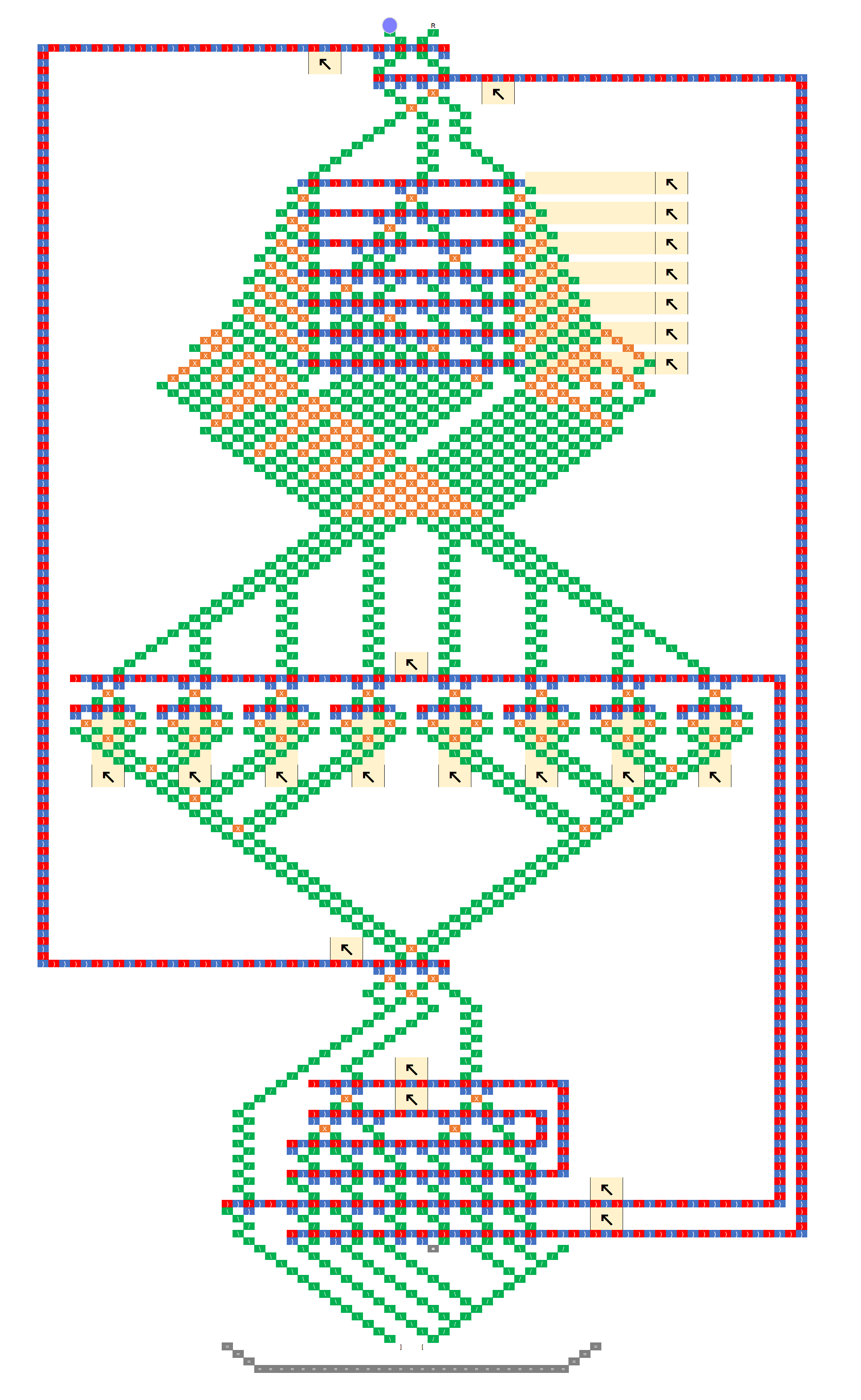
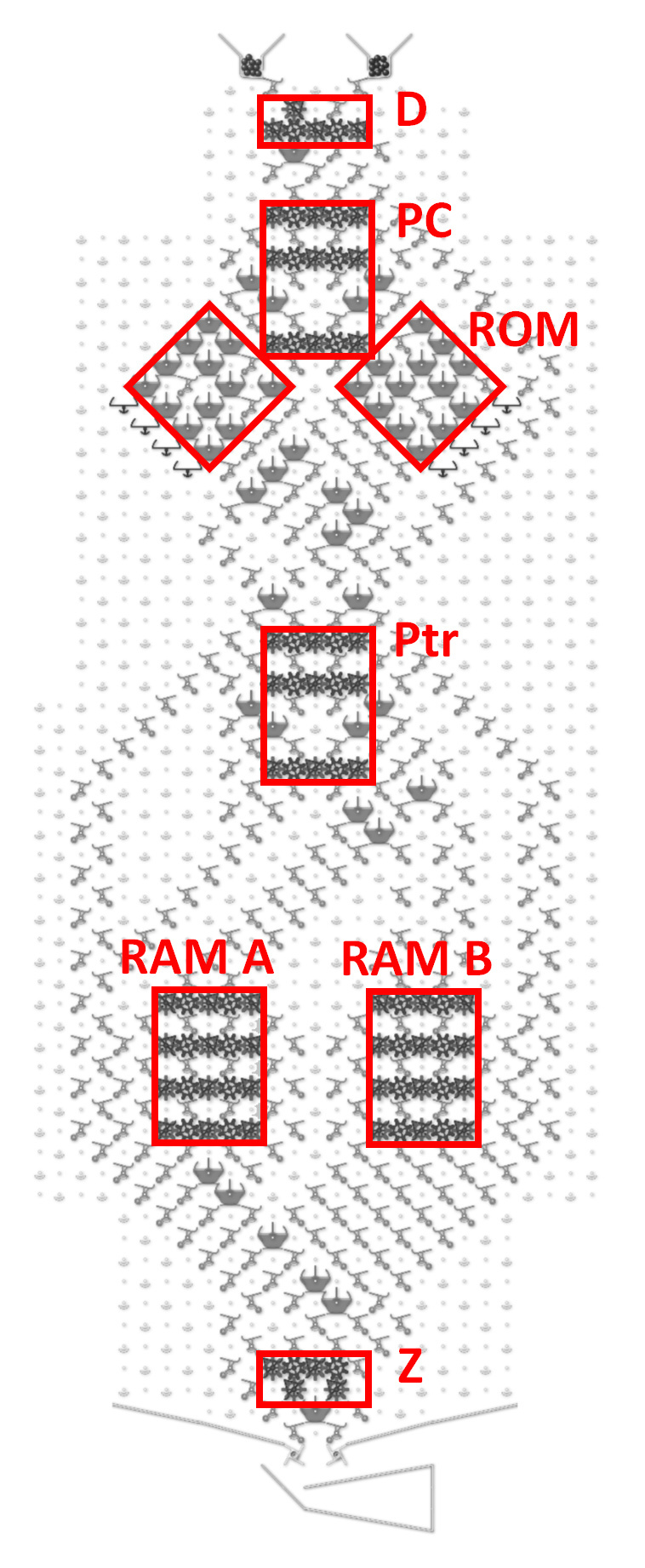
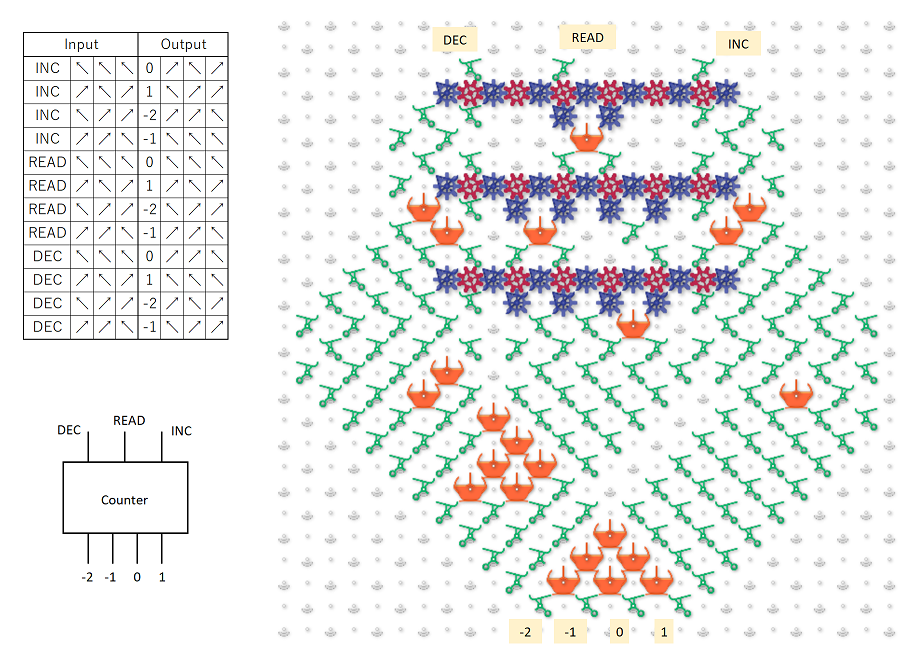
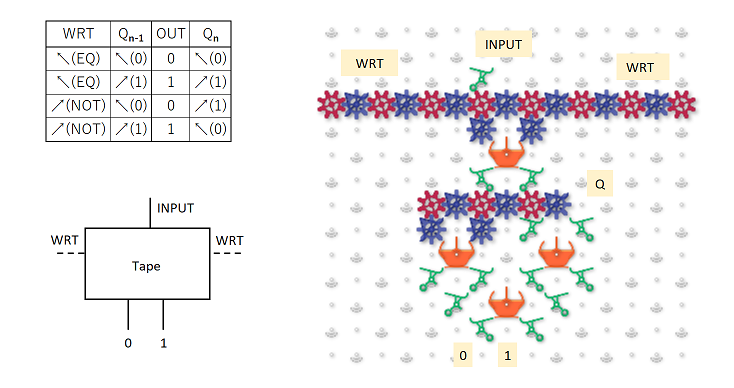
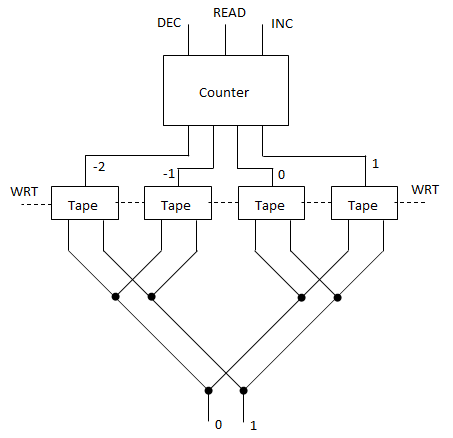
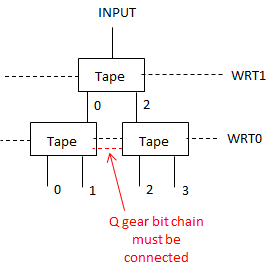
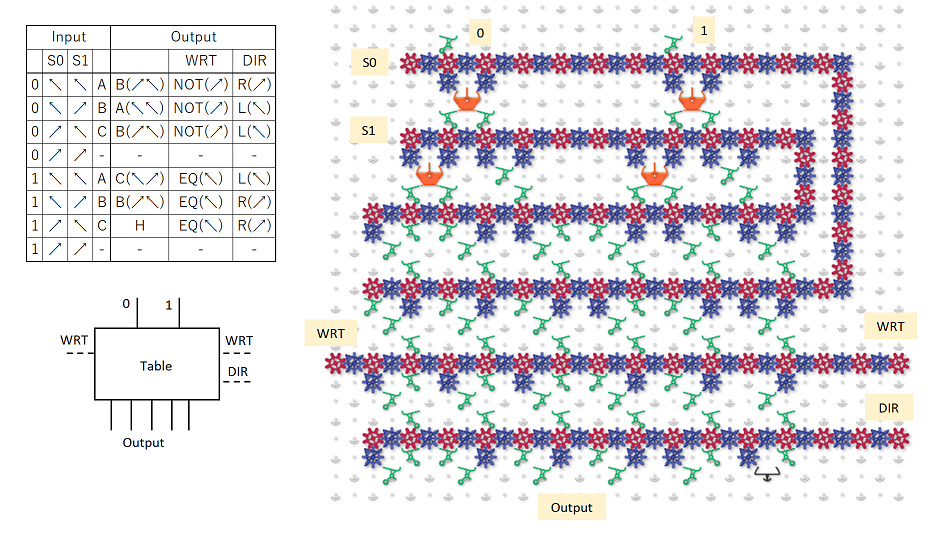
Before any ball drops, how is the state of the initial string represented? Is each “C” chain of gear bits flipped to 0 or 1 to indicate the value of the corresponding bit in the input?
-
When a ball drops in, what column does it drop into, and how is that achieved, both for the first, and for subsequent balls? If the initial string began 11011, then wouldn’t the ball need to feed into megapixel 1 in the 011 column (pretending that the nonexistent bit to the left were a 0)? How did it get there?
-
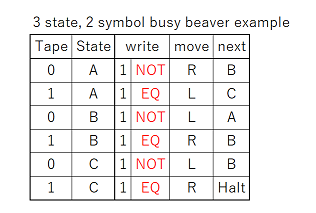
If the initial string were 11011, then upon arriving at megapixel 3, Rule 110 would indicate that the third bit should now change to a value of 1. How is that change represented? Wouldn’t the ball need to exit in column 111, which is not reachable from 101? Or would the ball be routed to 011, because that is the current generation’s values surrounding the fourth bit? And then the C chain representing the third bit would flip to a 1 to indicate the next generation value?
-
If the C chain of the third bit flips to a 1 per rule 110 after the ball passes through it, then isn’t the new value of 1 propagated via the C into bit 4’s megapixel? Doesn’t this affect the routing and update of bit 4, so that its update is based on the new value bit 3, and not the old value?
-
After a generation is updated, and a new ball is triggered, doesn’t the new ball have to find its way to the correct column indicating the value of the first two bits (edge condition). I.e., if the new generation began 11, then assuming we’re treating the nonexistent left neighbor of the first bit as a 0, wouldn’t the ball need to find its way to column 011?
As you can see from the above questions, I’m pretty confused. Any light you can shed on this would help me. This is very intriguing indeed.
p.s. I love the schematic representation.
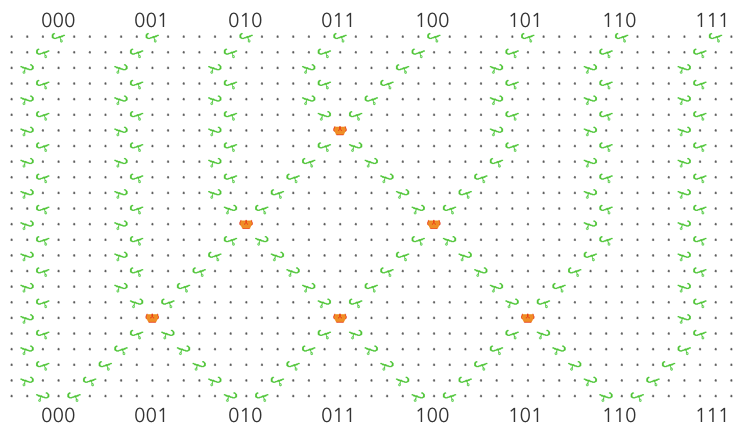
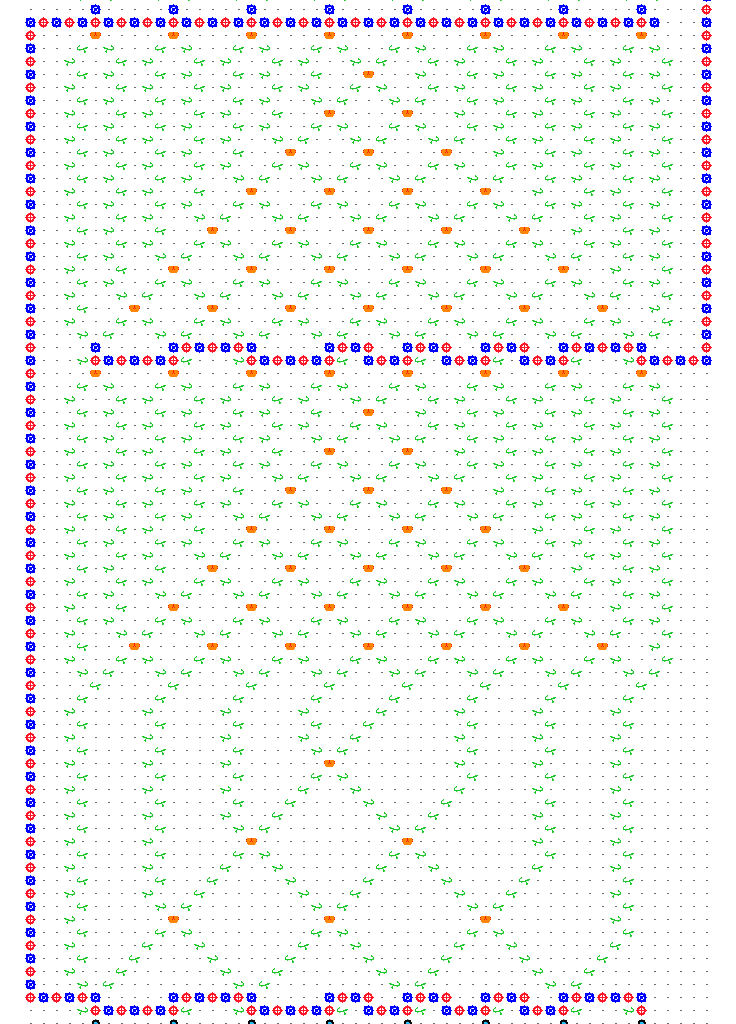
 , S1 =
, S1 =  }
}