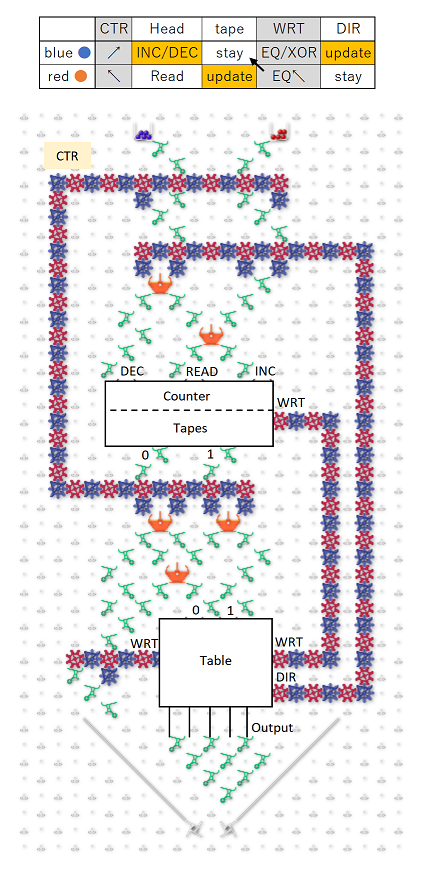
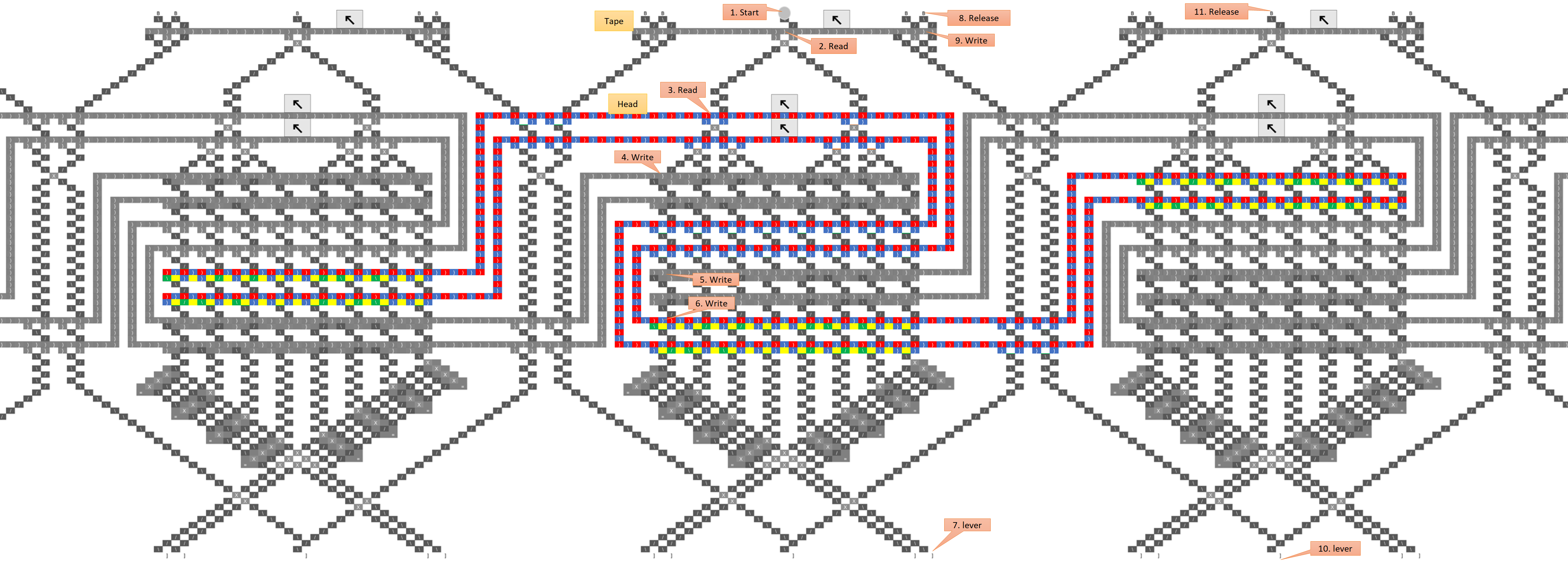
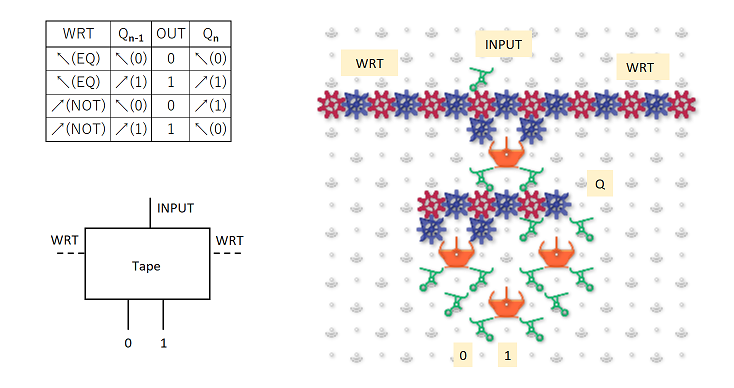
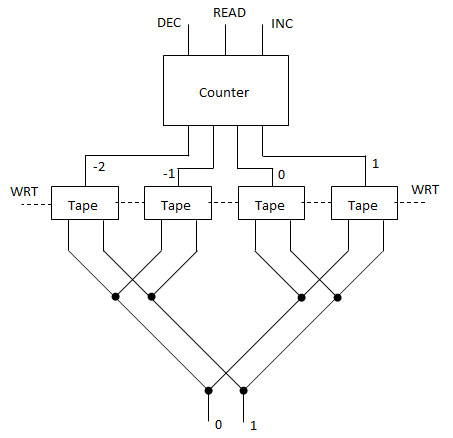
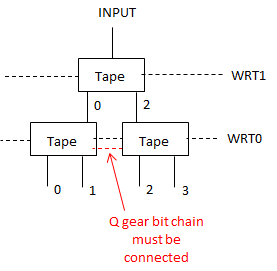
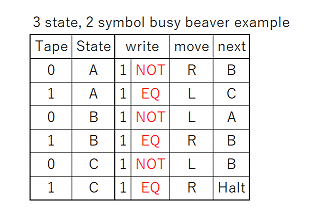
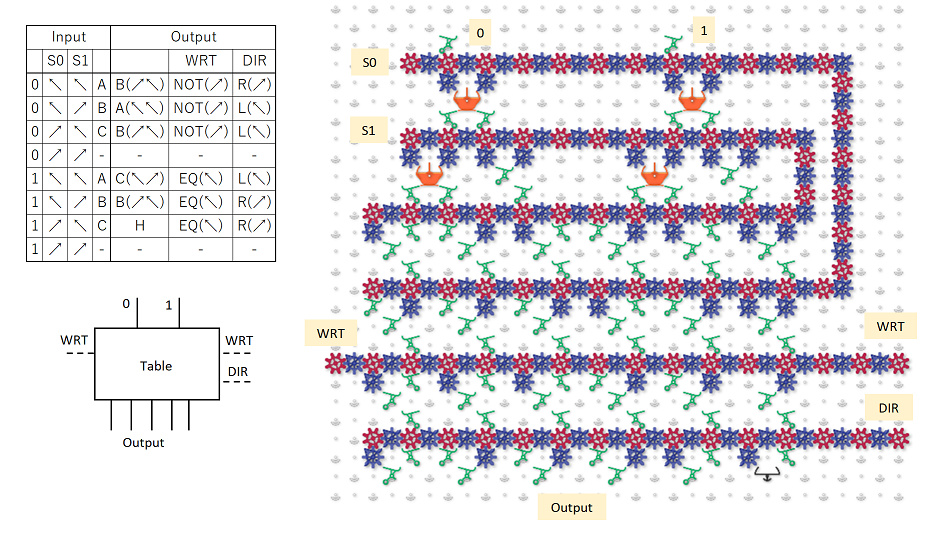
I haven’t had a chance to digest this yet. But, I was thinking about how to extend what I did in another post (computing any Boolean function of N bits to 1 bit) so that it could compute any function from N bits to N bits. It is easily extended, and, using your “C” idea, the output can be piped back up to the input bits, creating a feedback loop. You need N nested Cs. A decision tree is used at the top to divide into 2^N paths (in your language, we’re “pushing” N bits). Then, we just write the N bits. So, I think this is a simpler way of doing what you’re trying to do, since we can encode any funciton (including those corresponding to cellular automata).
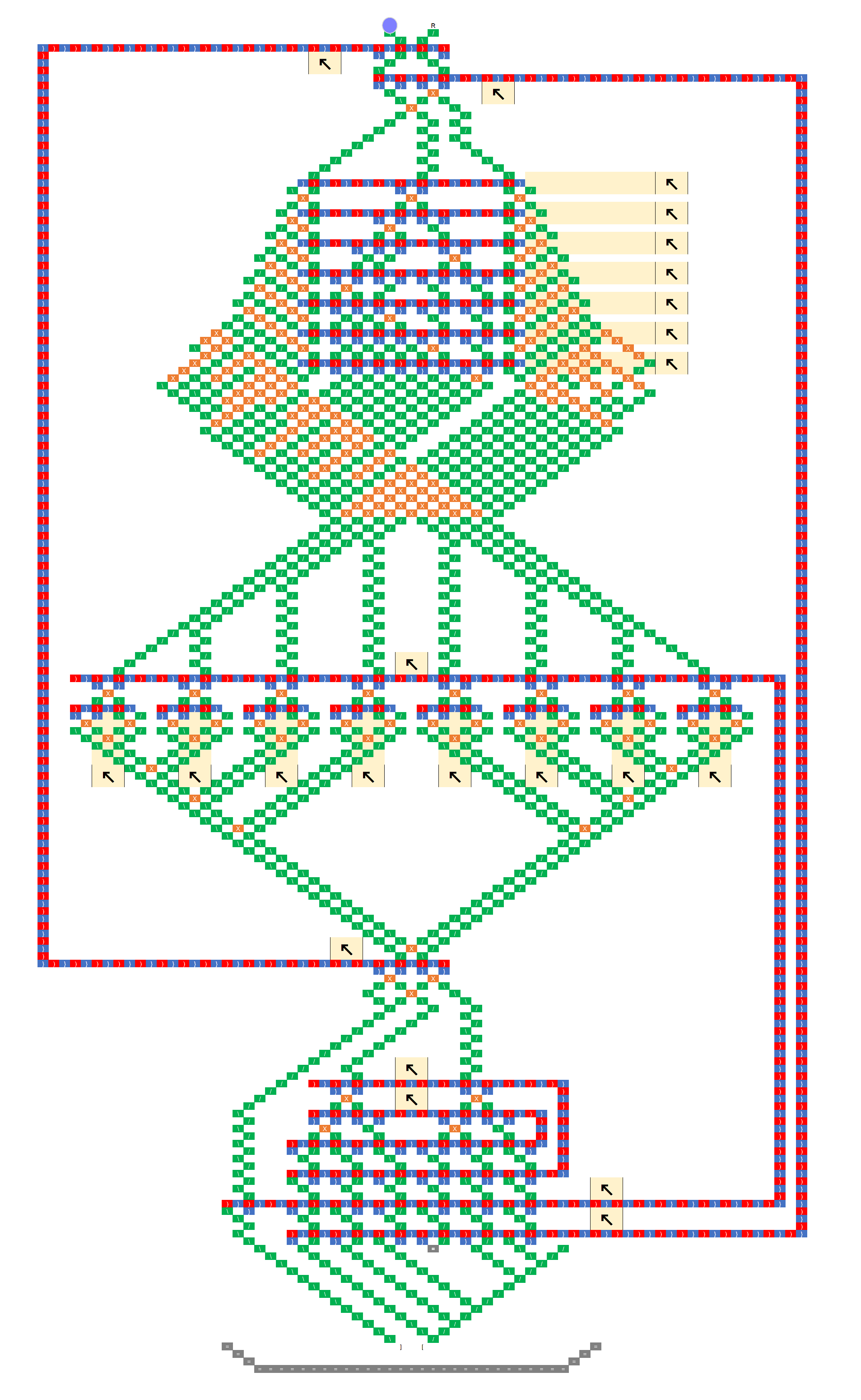
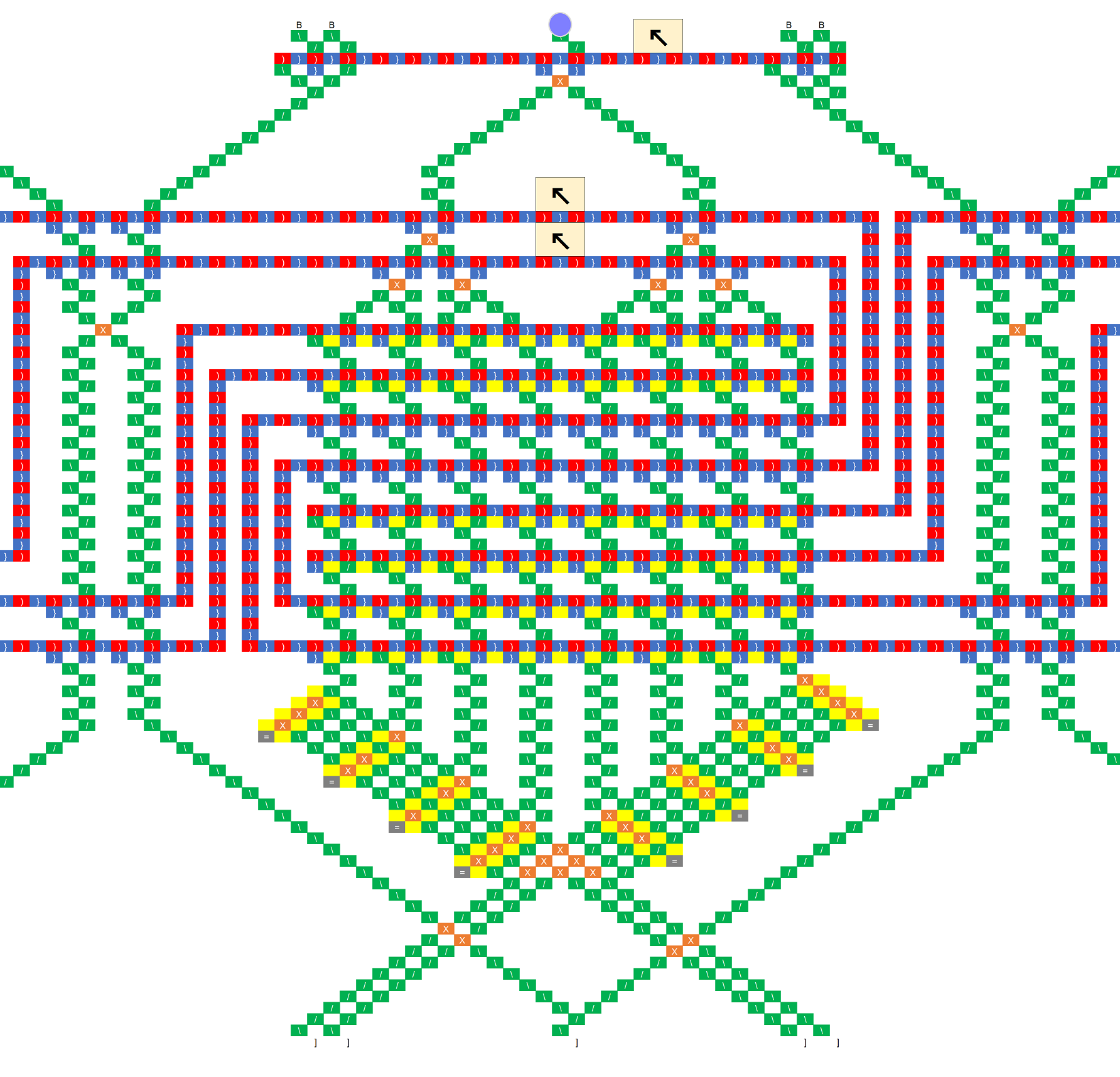
I tried to create a demo of 3 bits to 3 bits with the feedback loop, and ran tight on space because I couldn’t yet get the tree to spread out enough. But, I do have it working for six of the eight possible inputs -for some inputs, I’m just intercepting the ball. (Note: the innermost feedback “C” isn’t a “C” - space ran tight so I had to modify it a bit so it is an upside down U.)
It is here.
I’m not sure what function is encoded - I made it somewhat arbitrary, and in some cases, I ran out of space and things should be more spread out, so chose a value to output that used less space. and didn’t interfere with another path. In other places, I just terminated the path with an interceptor. But, if you set the input so that the first bit is 1, then it will work just fine. On the other side of the tree, there is only one input that is not intercepted. I might be able to redraw this to make it complete by shifting everything a little bit, but I didn’t have the energy and have out of town guests arriving, so that will be another day.

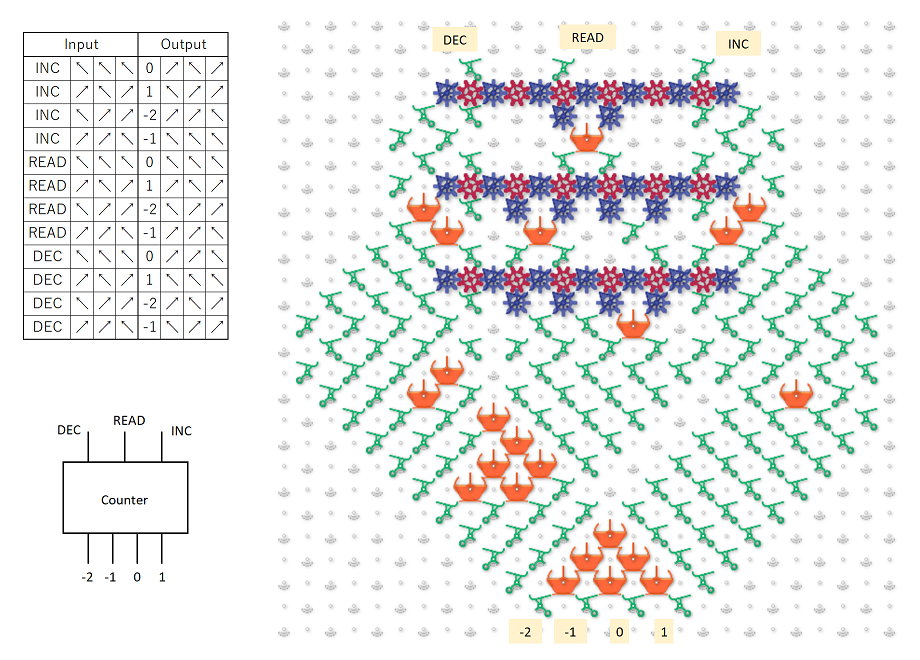
 , S1 =
, S1 =  }
}